Beautiful Tips About How To Find The Best Fit Line In A Linear Regression Model Add Second Y Axis Excel Chart

Fit a linear model to the data.

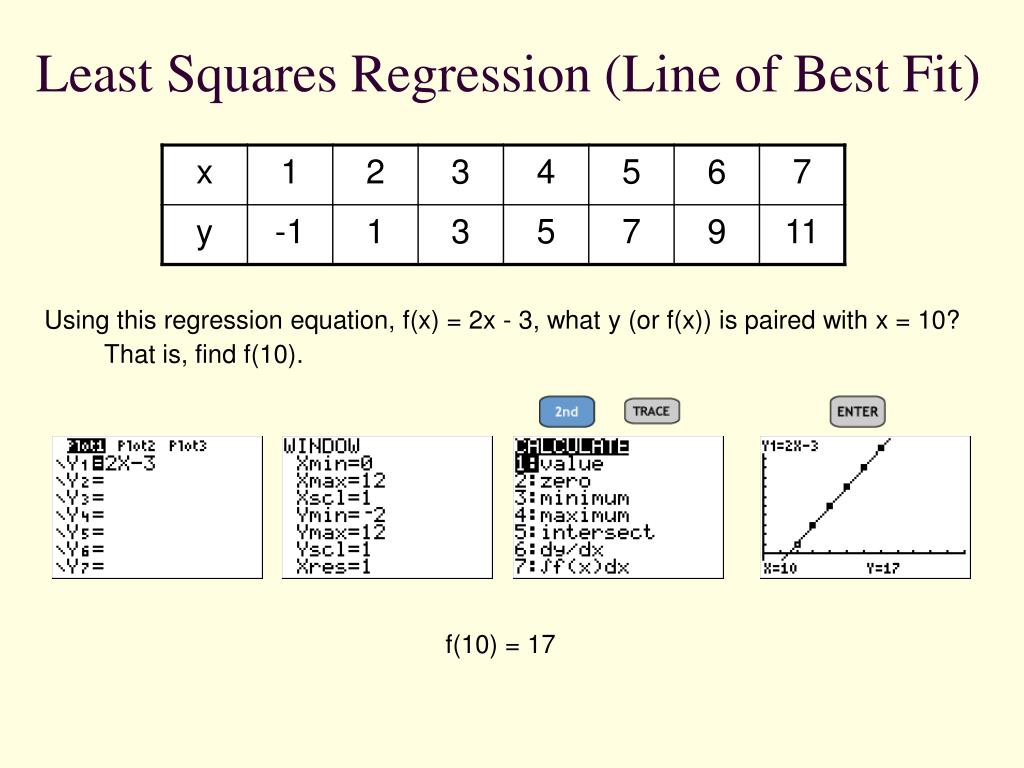
How to find the best fit line in a linear regression model. Write a linear equation to describe the given model. Estimate the slope parameter, b1, using equation 7.3.4. We can use the line to make predictions.

This model equation gives a line of best fit, which can be used to produce estimates of a response variable based on any value of the predictors ( within reason ). Xi = current value of x. First the training data, which should be a 2d array, and second the target values.

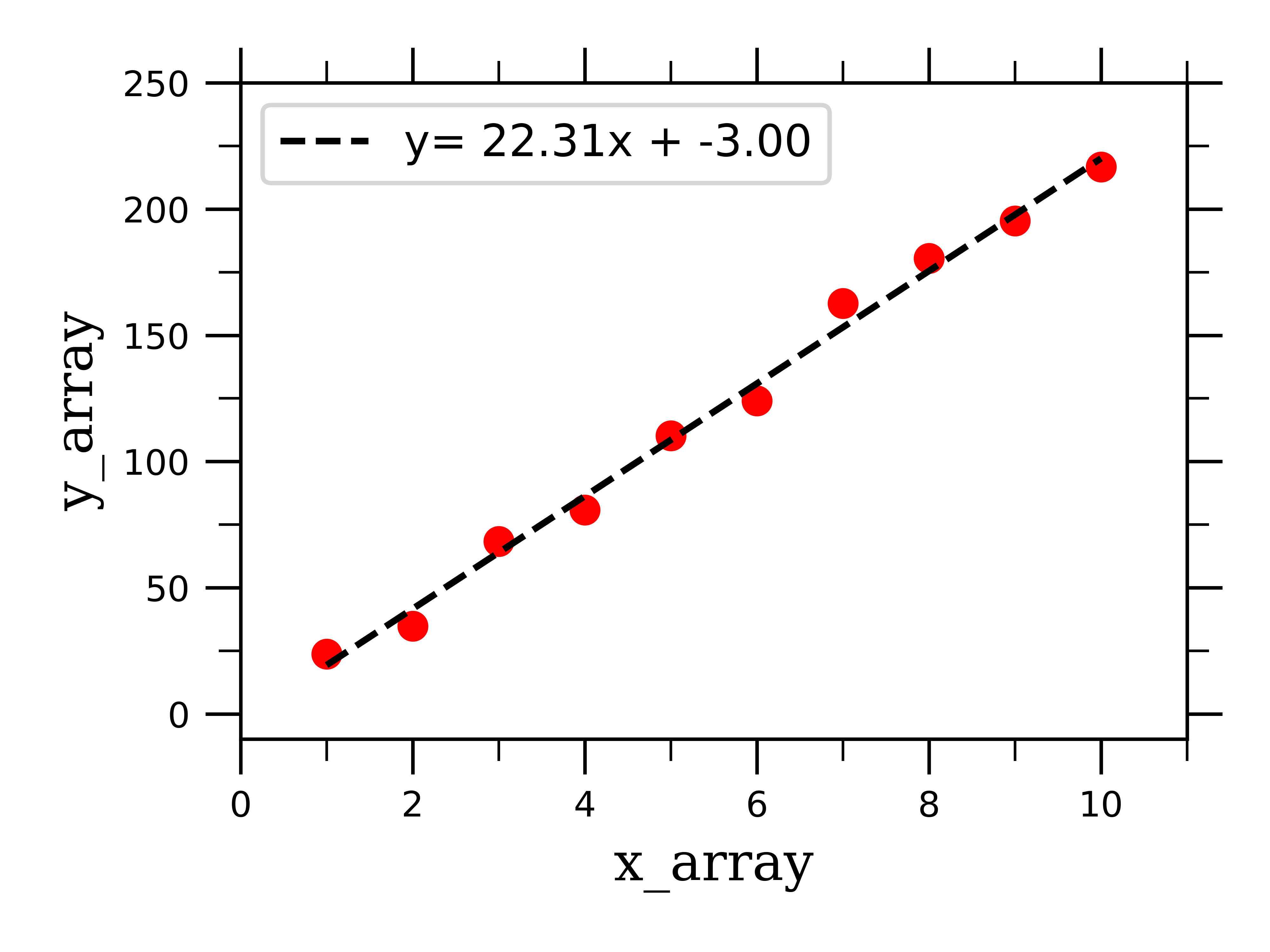
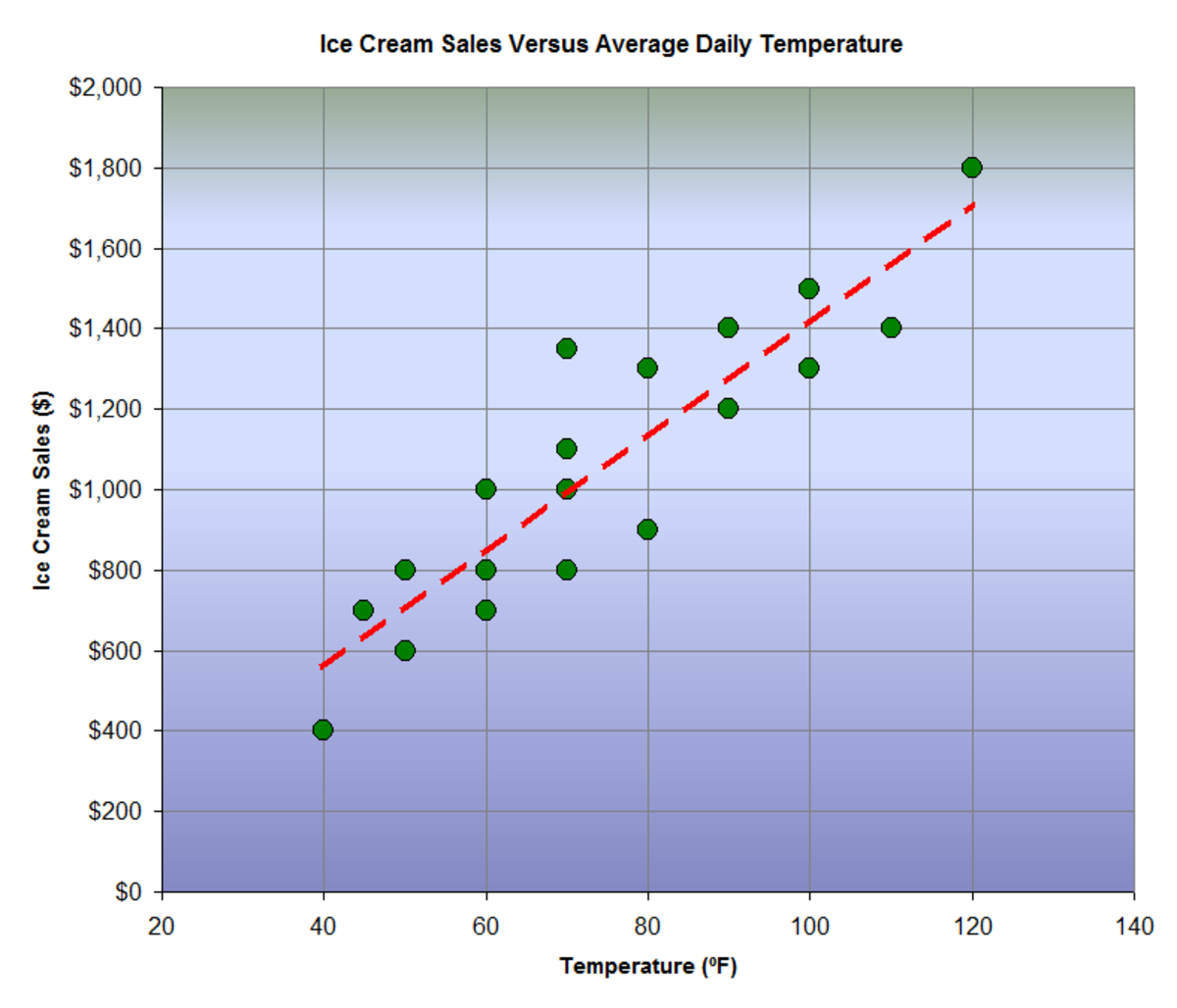
The equation of the best fitting line is: This example shows how to perform simple linear regression using the accidents dataset. We can't ignore points that don't fit the trend.

Y ^ i = b 0 + b 1 x i. This article will discuss the following metrics for choosing the ‘best’ linear regression model: I’ll show you those later in this post.

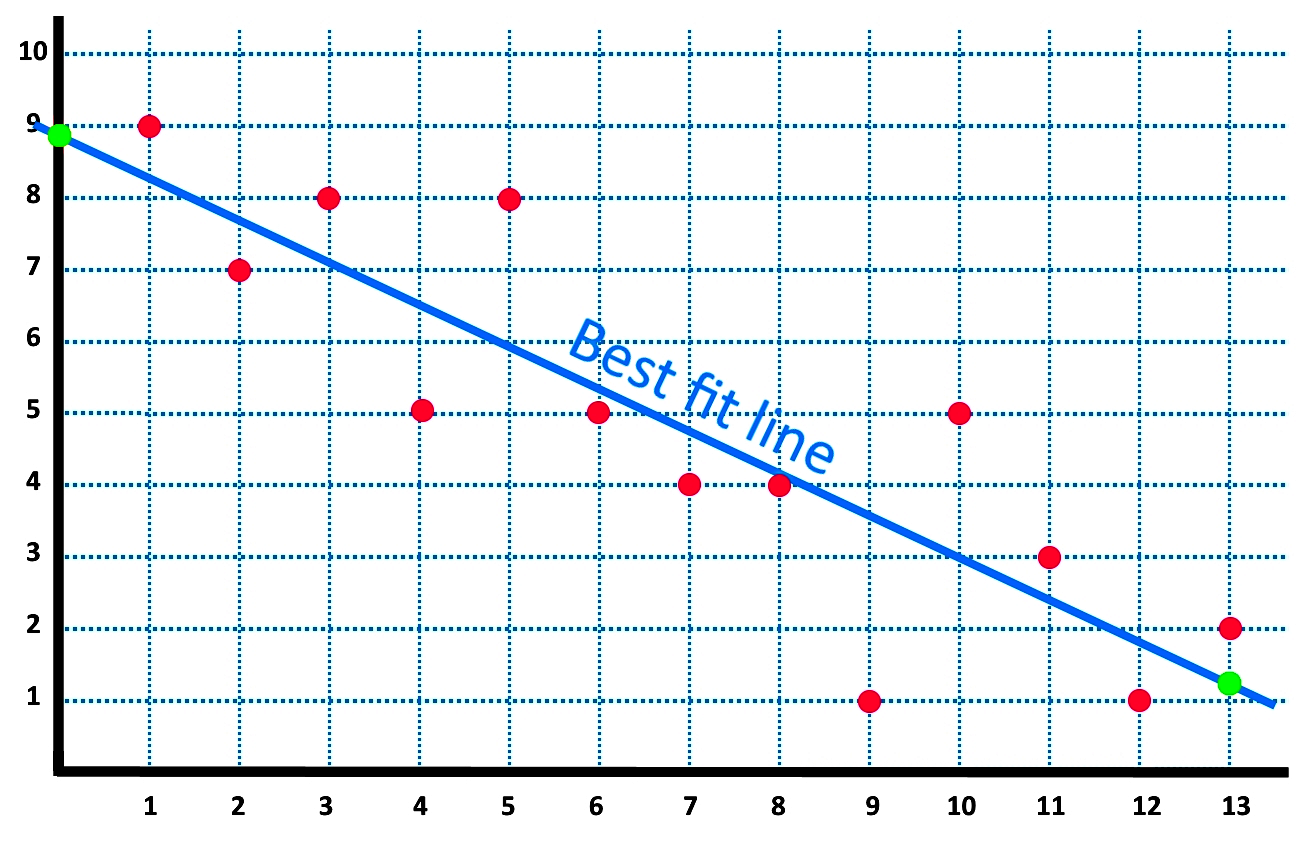
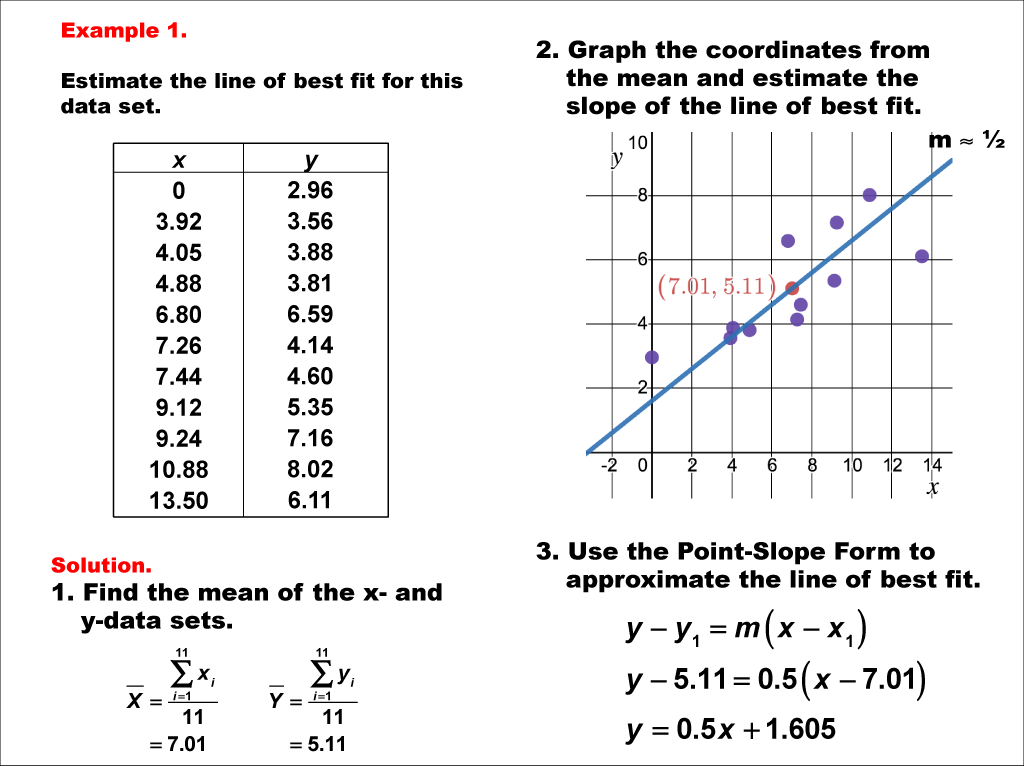
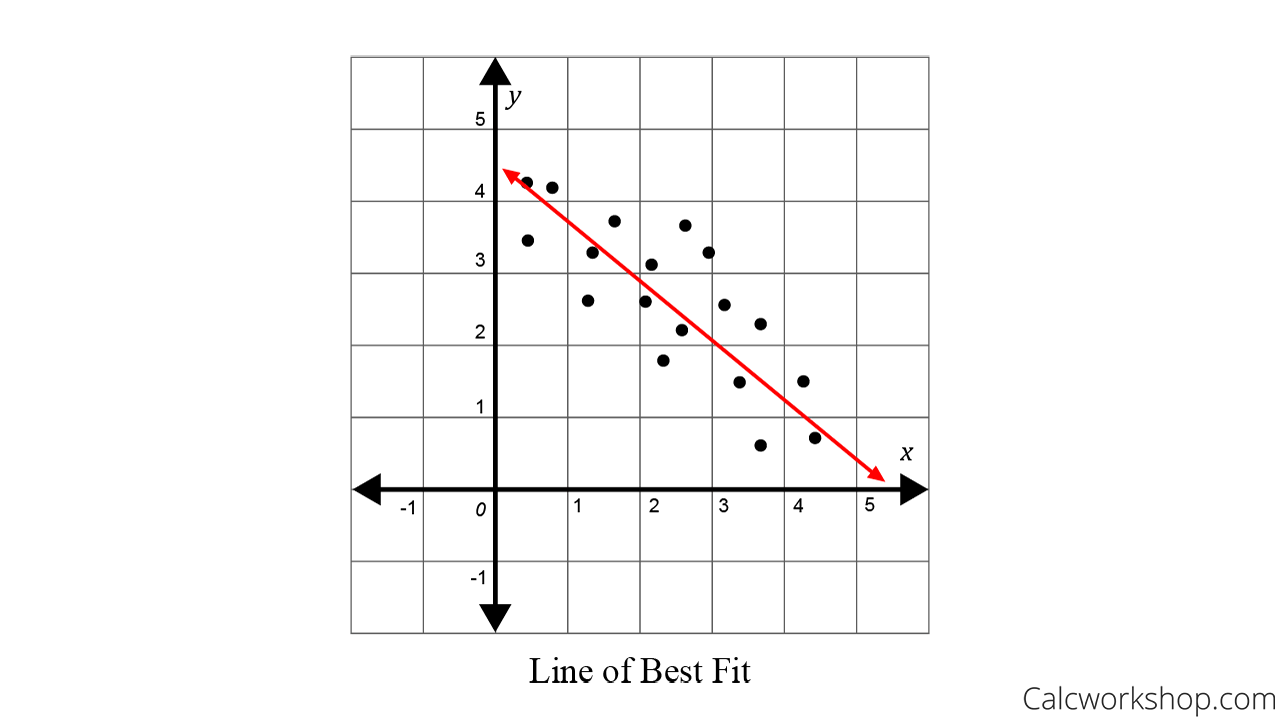
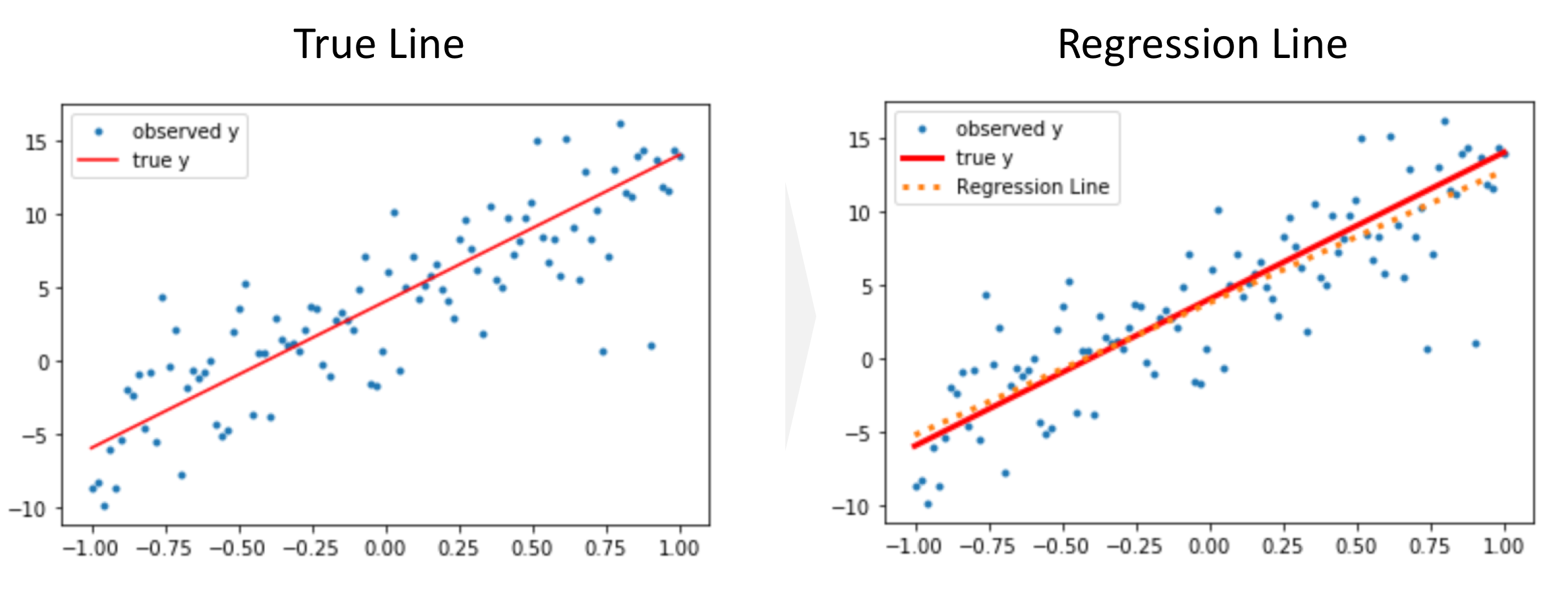
Where, x bar = mean value of x. A line was fit to the data to model the relationship. The line of best fit is used to express a relationship in a scatter plot of.

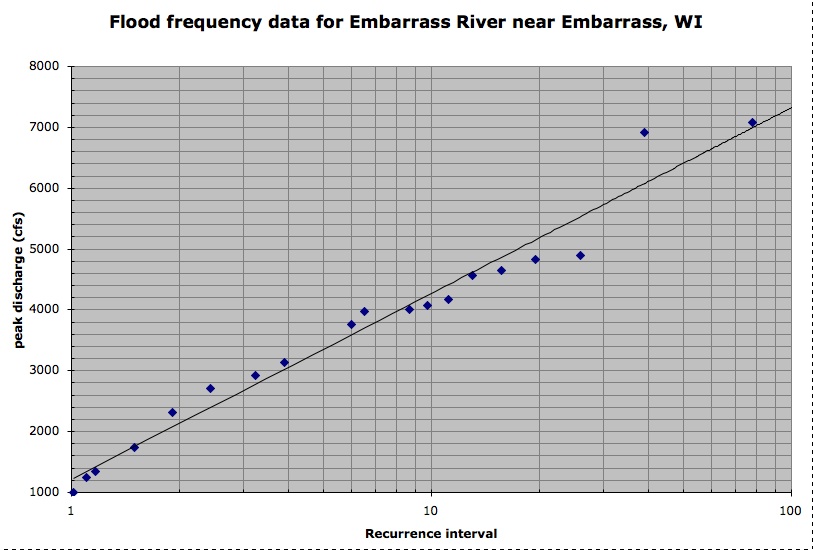
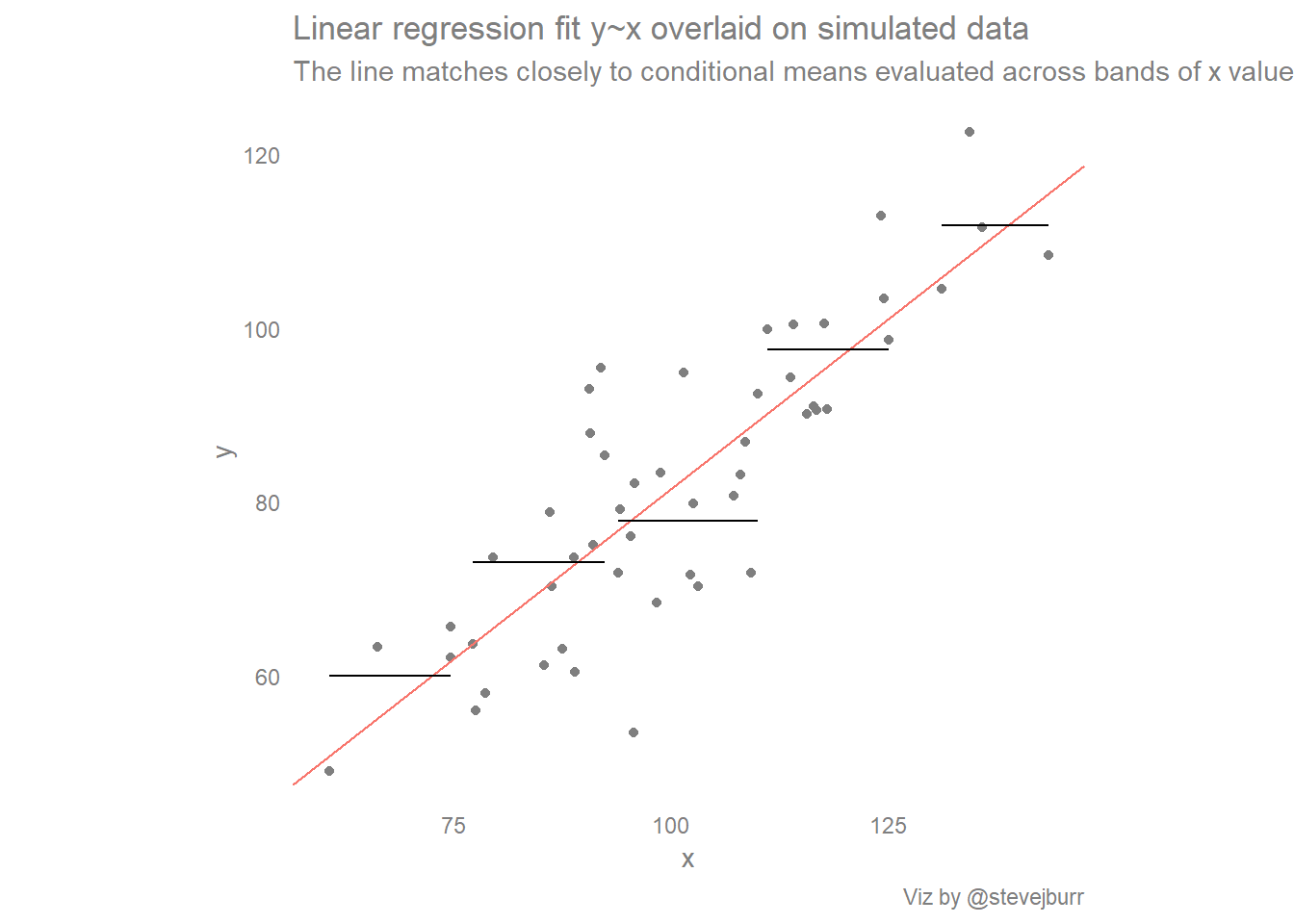
It also produces the scatter plot with the line of best fit. The linear regression model attempts to find the relationship between variables by finding the best fit line. The line of best fit (or trendline) is an educated guess about where a linear equation might fall in a set of data plotted on a scatter plot.

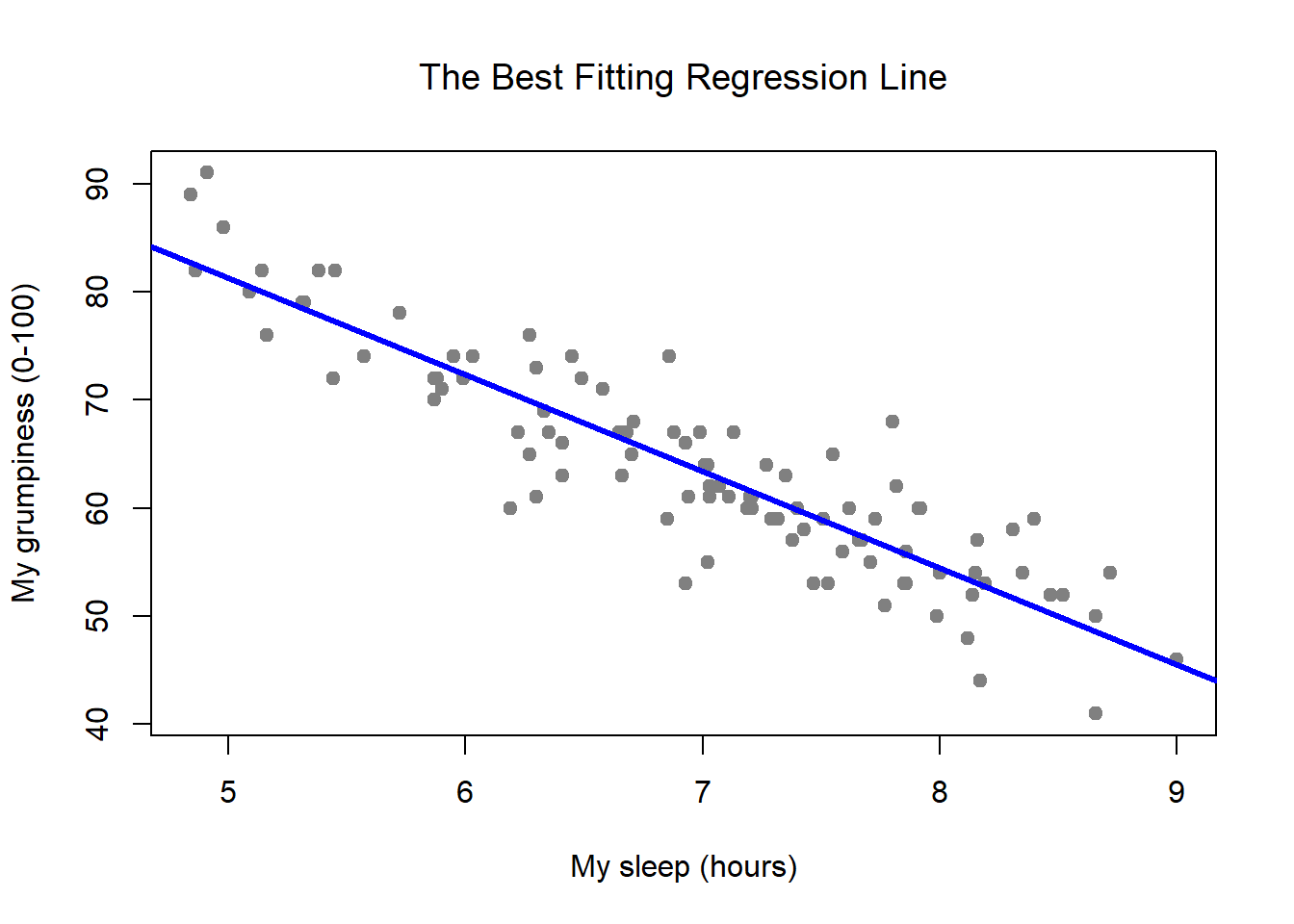
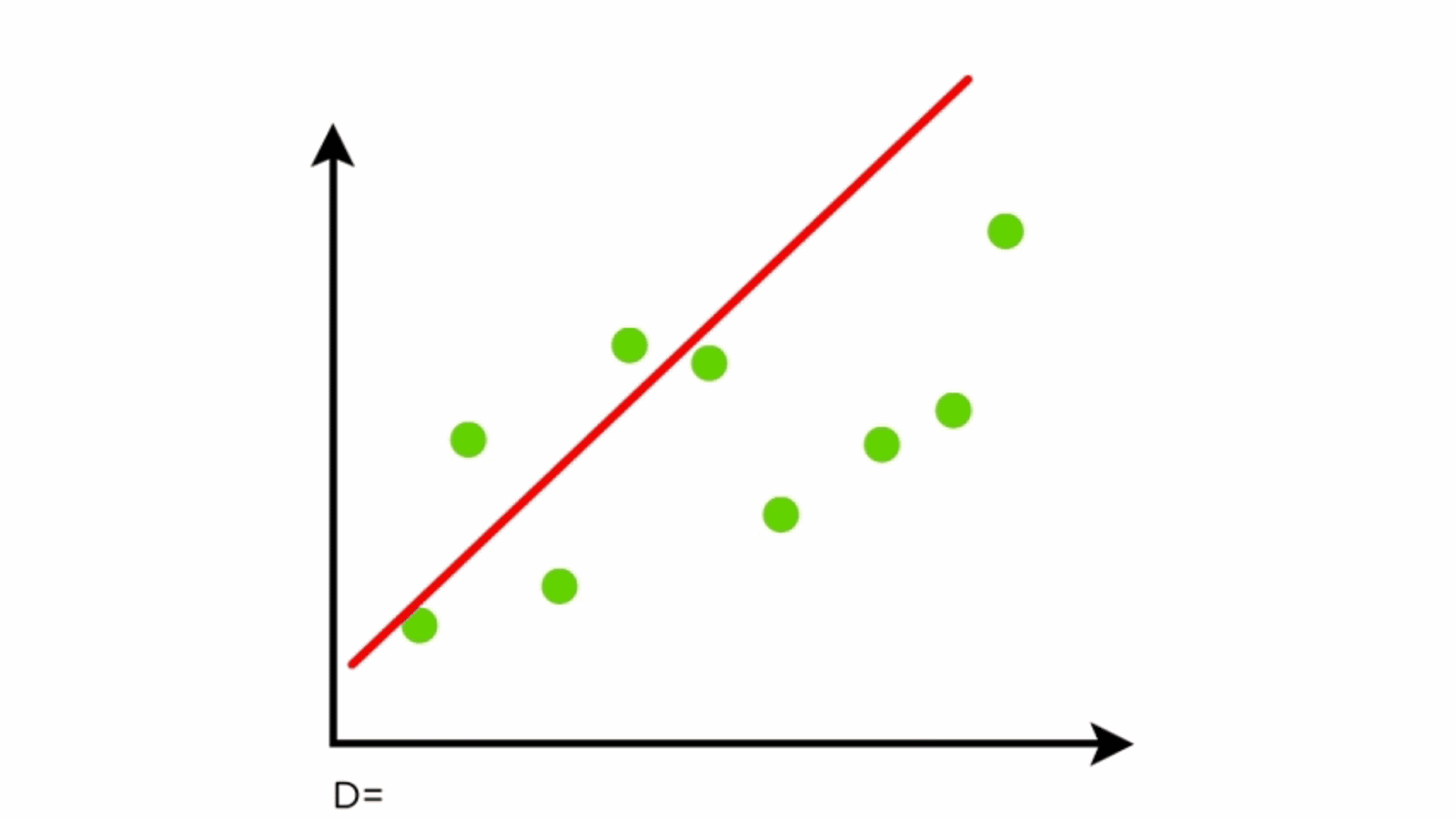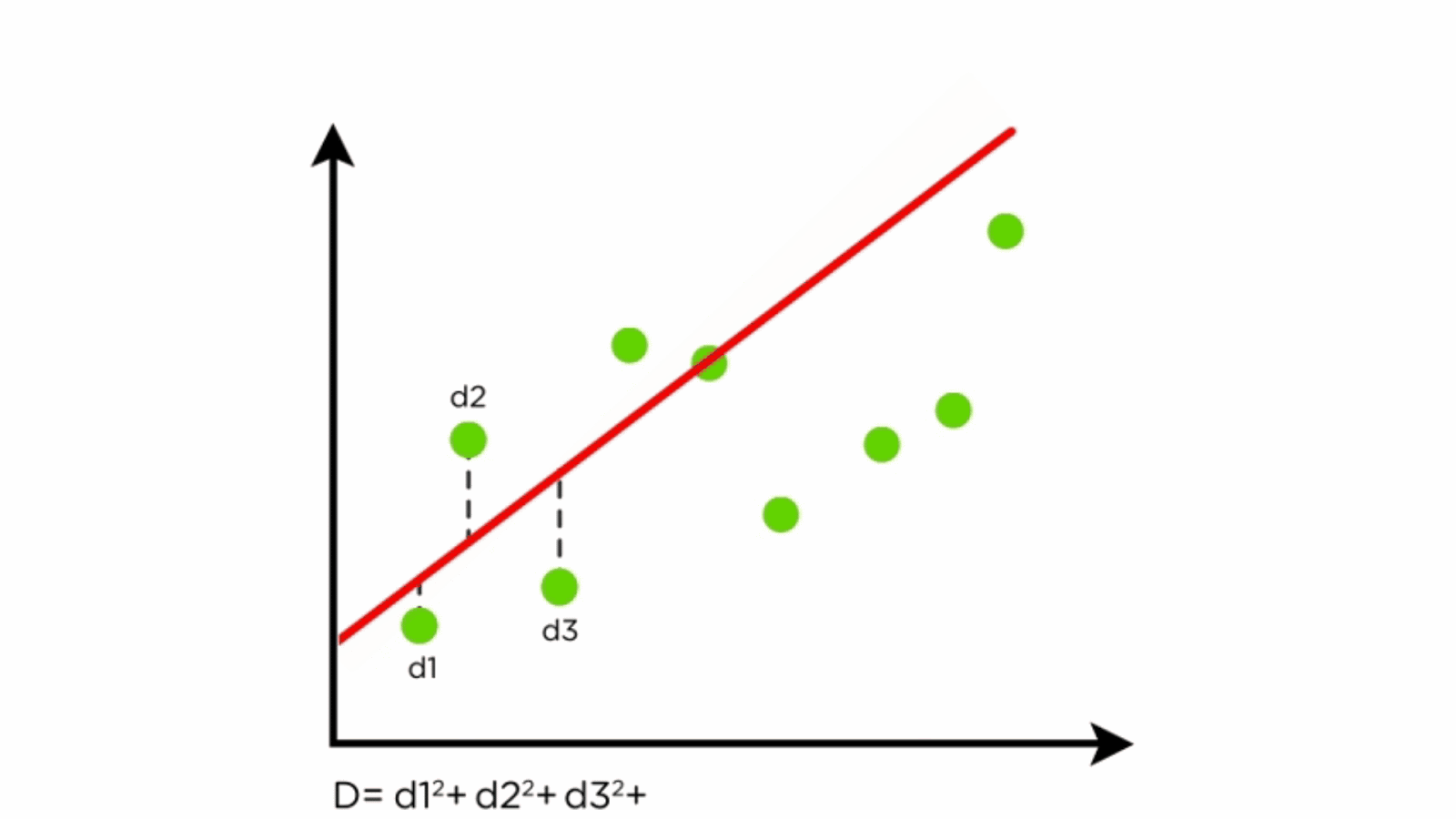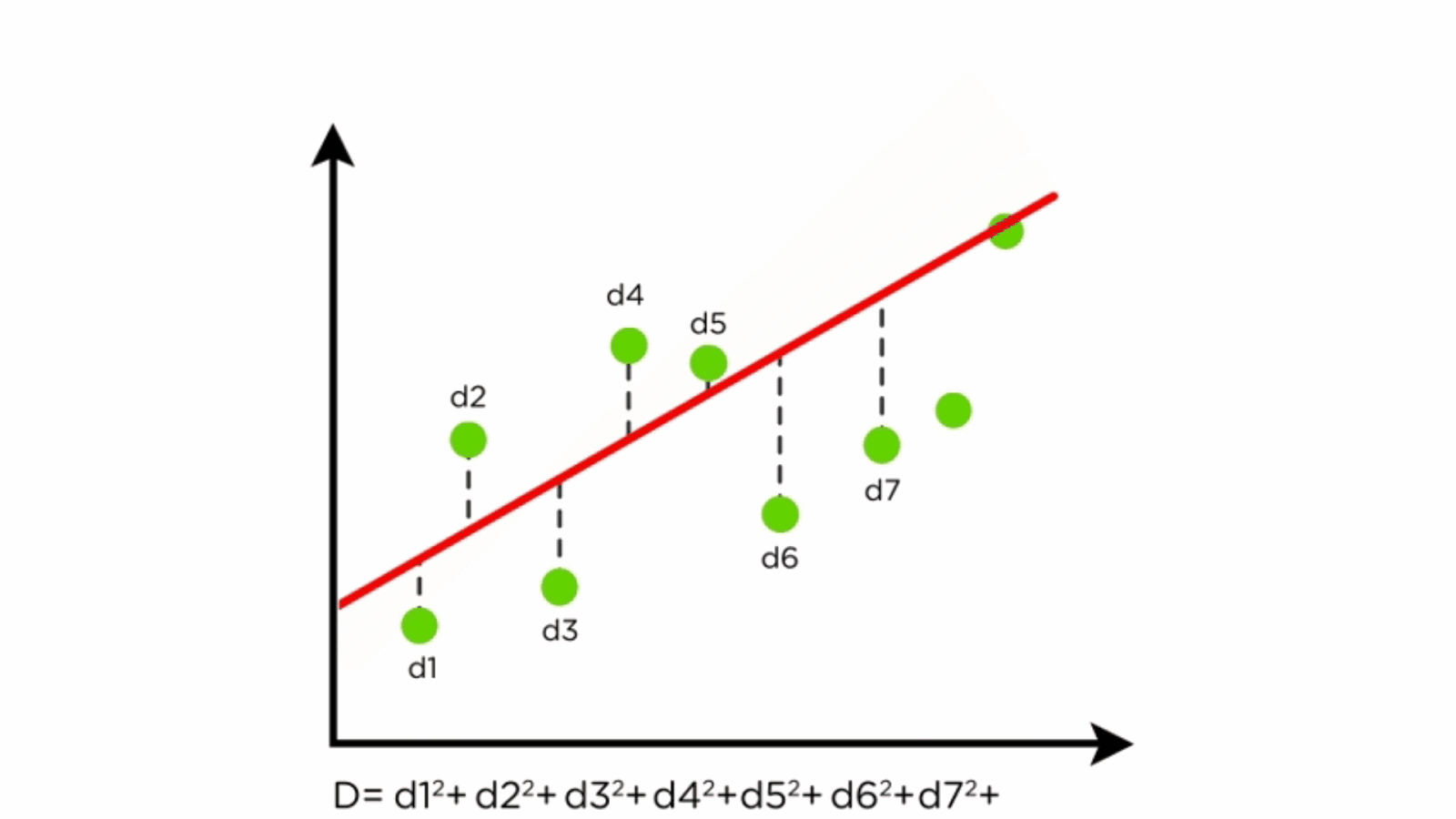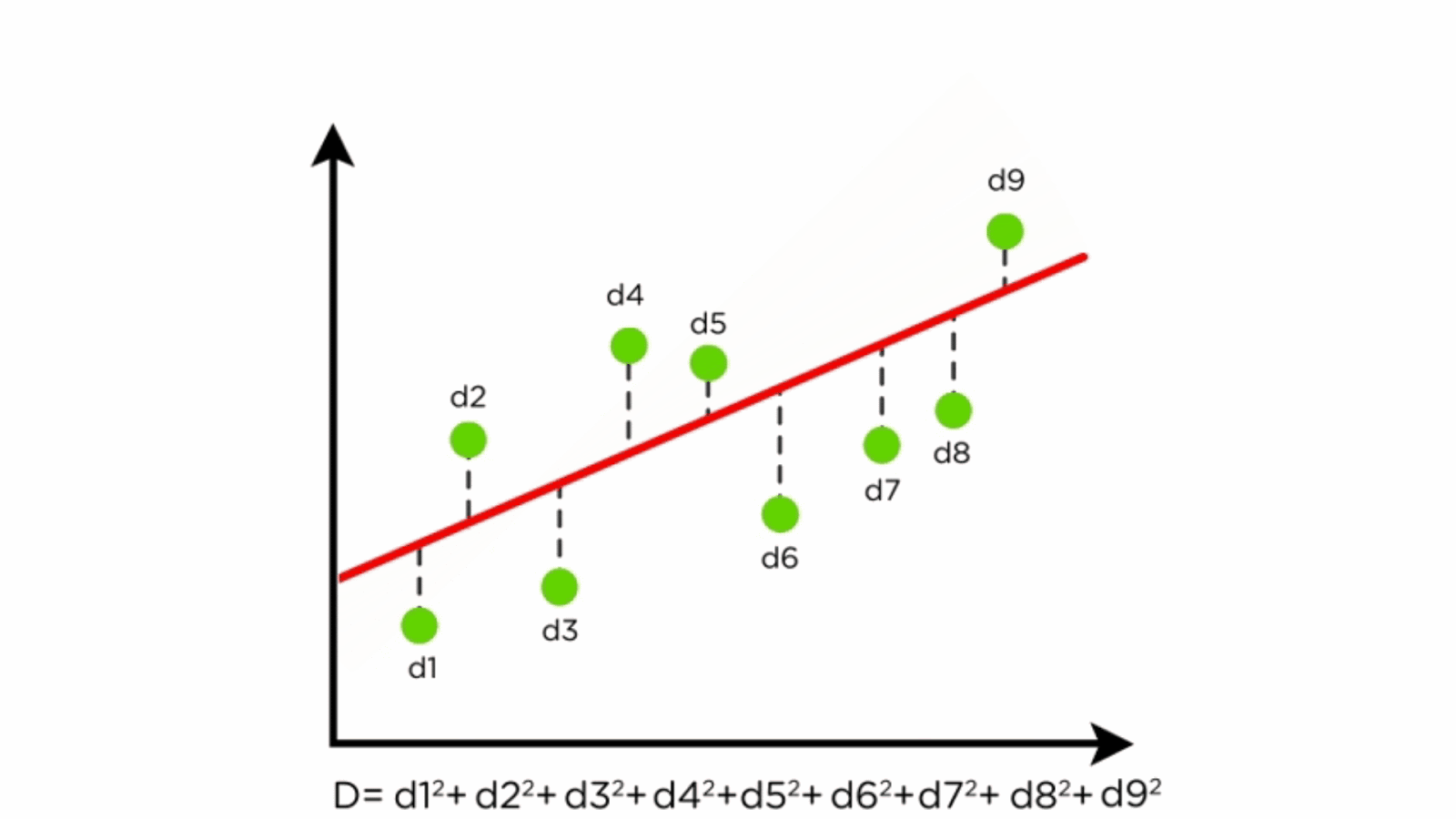
We often display them in a residual plot such as the one shown in figure \(\pageindex{6}\) for the regression line in figure \(\pageindex{5}\). In the case considered here, we simply what to make a fit, so we do not care about the notions too much, but we need to bring the first input to that function into the desired shape. The calculator above will graph and output a simple linear regression model for you, along with testing the relationship and the model equation.

Residuals are helpful in evaluating how well a linear model fits a data set. You need to make a choice which model you want to use. The sklearn.linearregression.fit takes two arguments.

Least squares is a method to apply linear regression. Q = ∑ i = 1 n ( y i − y ^ i) 2. Find out which linear regression model is the best fit for your data.

Y bar = mean value of y. In this post, i’ll define a least squares regression line, explain how they work, and work through an example of finding that line by using the least squares formula. A line of best fit is a straight line that minimizes the distance between it and some data.