First Class Info About How To Interpret A Line Fit Plot Time Series In R With Dates

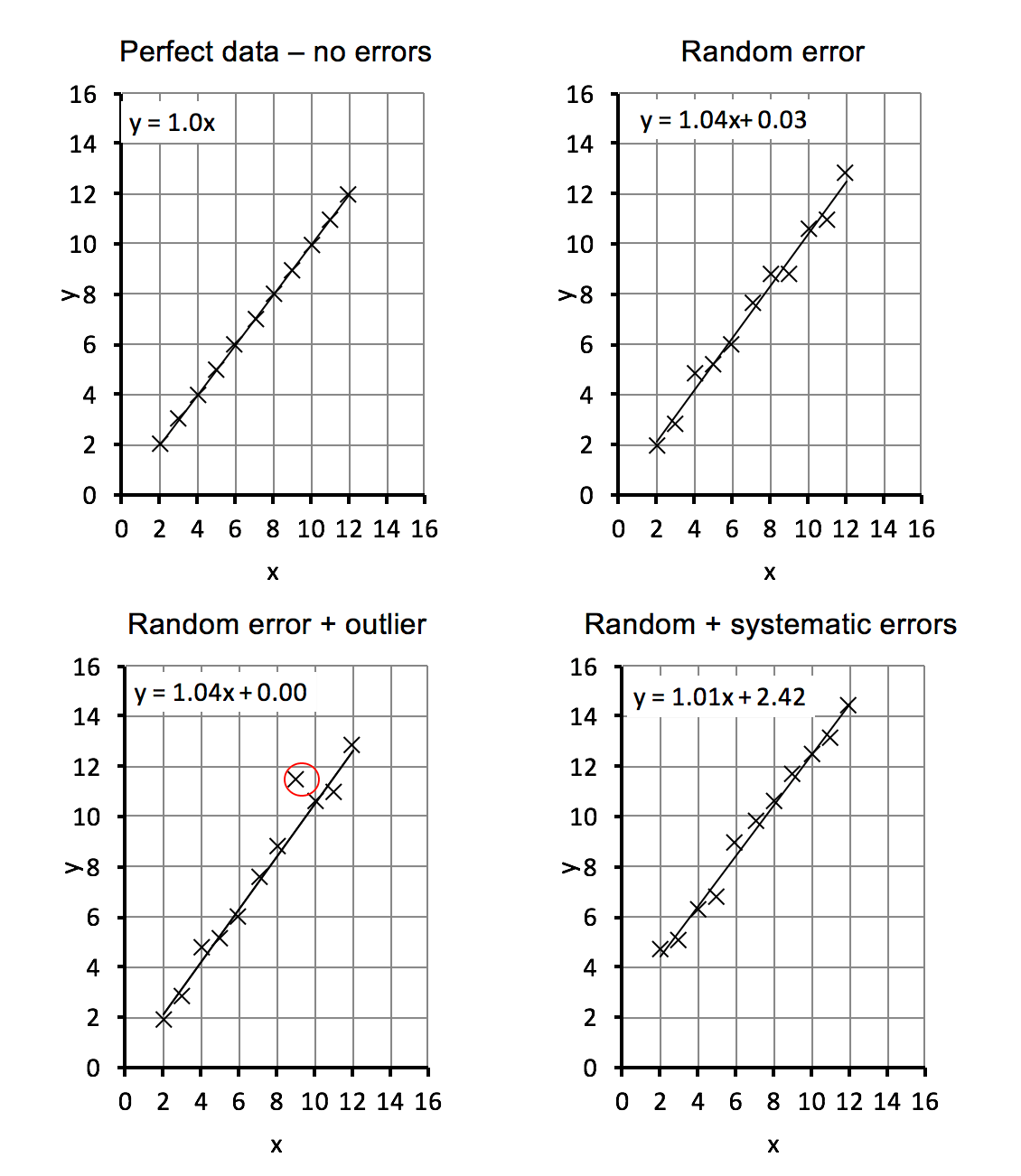
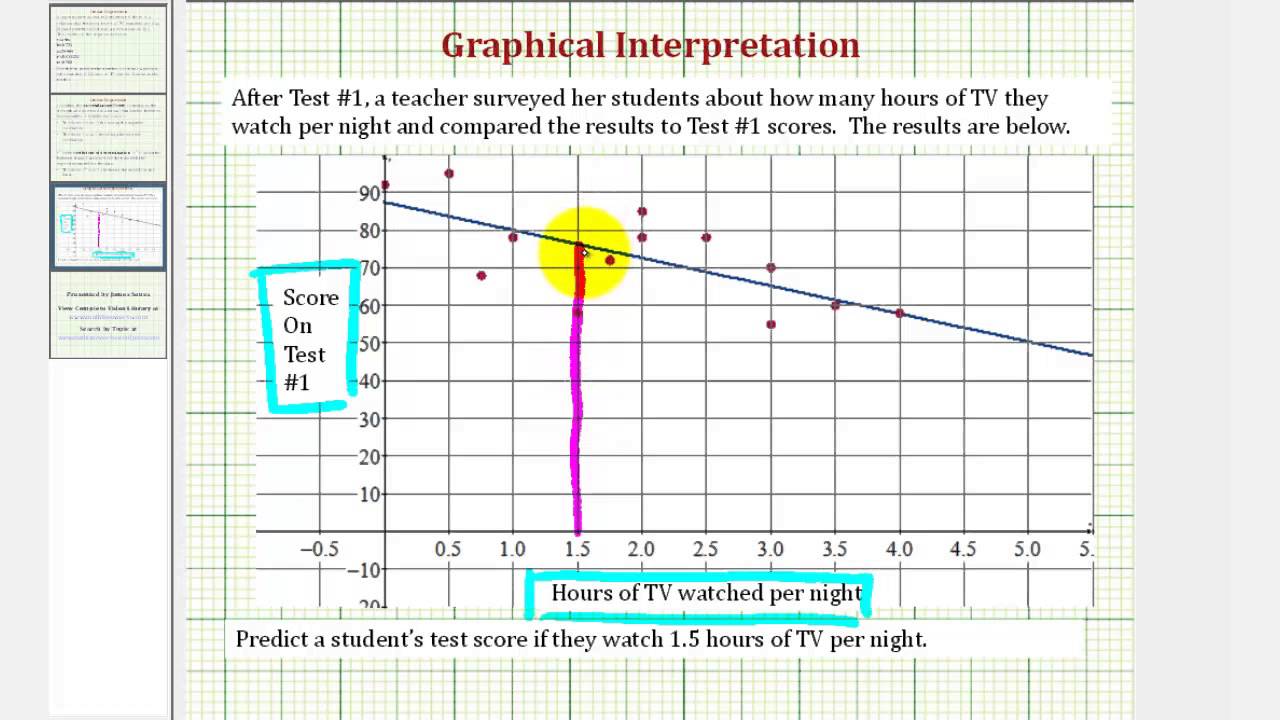
The fitted line plot displays the response and predictor data.

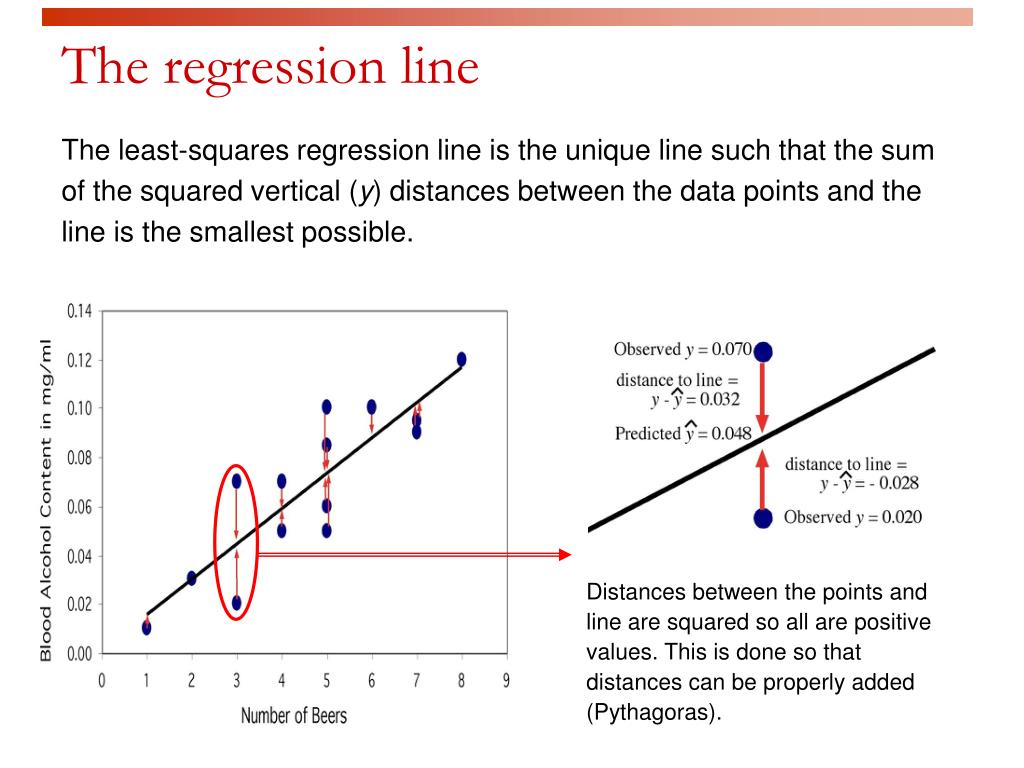
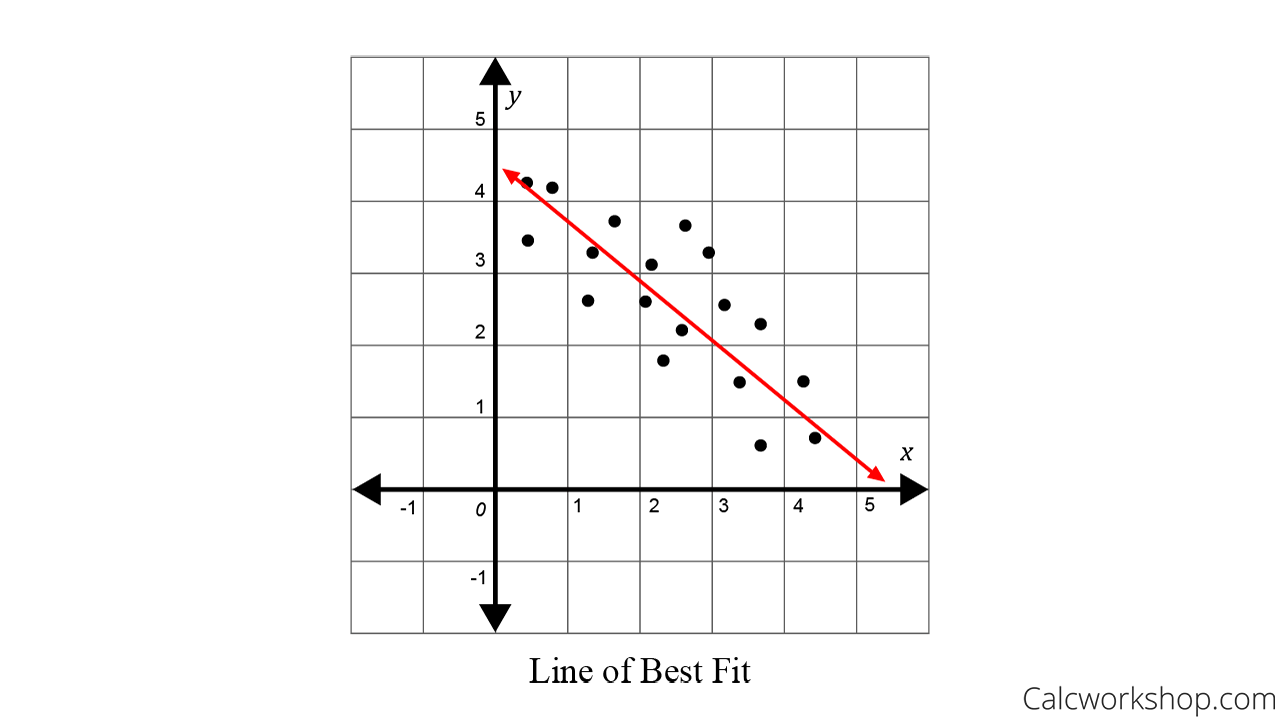
How to interpret a line fit plot. Beginning with straight lines; Add the line of best fit. A fitted line plot of the resulting data, ( alcohol arm data ), looks like this:

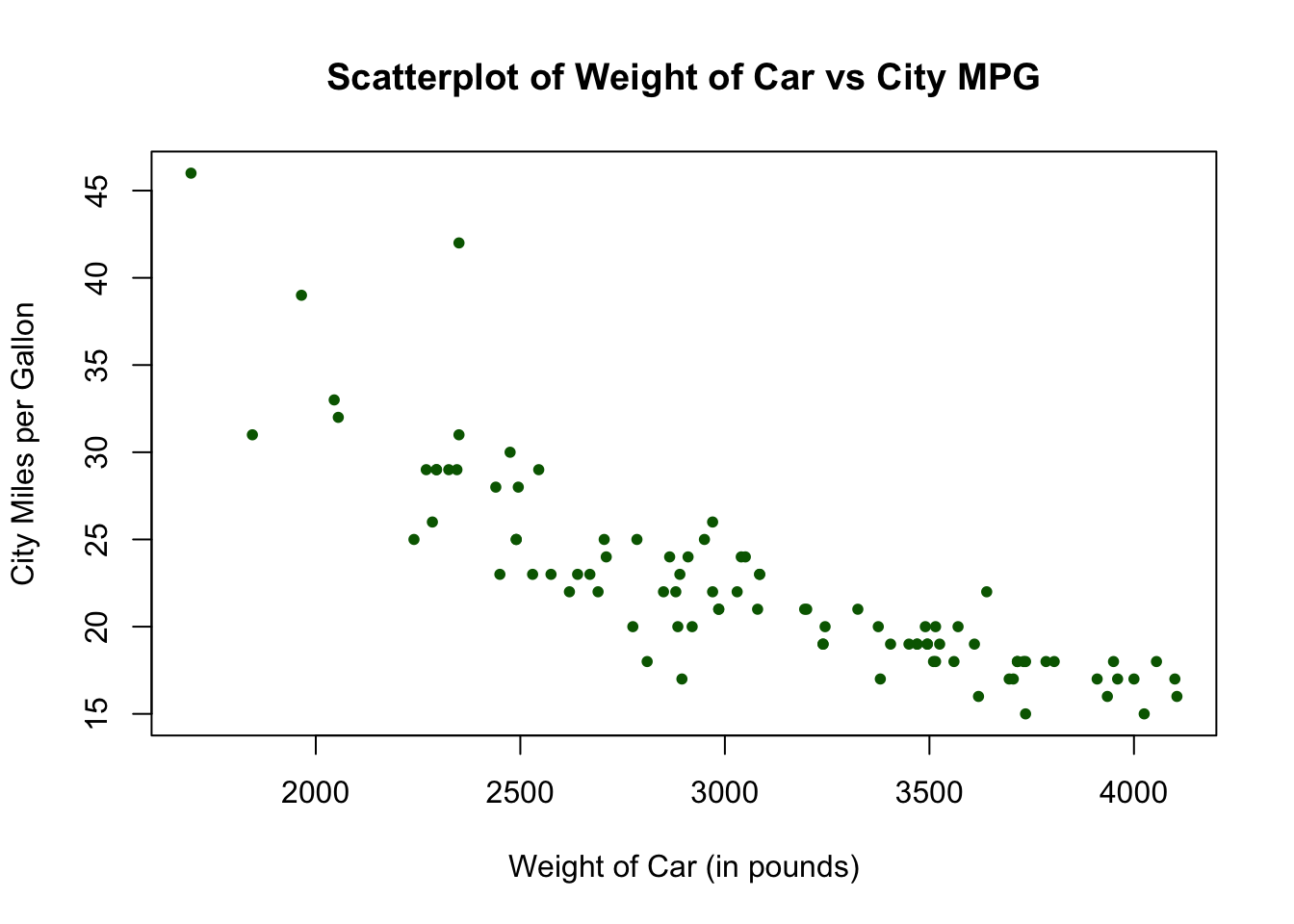
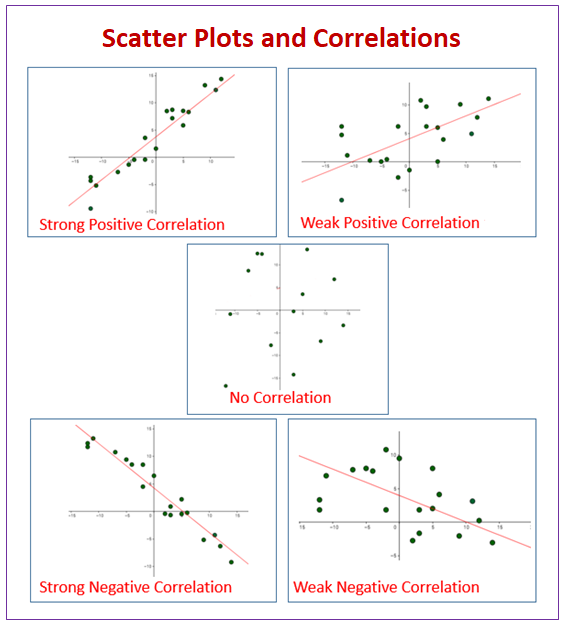
A line of best fit is a straight line that minimizes the distance between it and some data. The plot suggests that there is a decreasing linear relationship between alcohol and arm. Display main and interaction effects.

In predictor (x), enter density. In response (y), enter stiffness. A line of best fit can be drawn on the scatter.

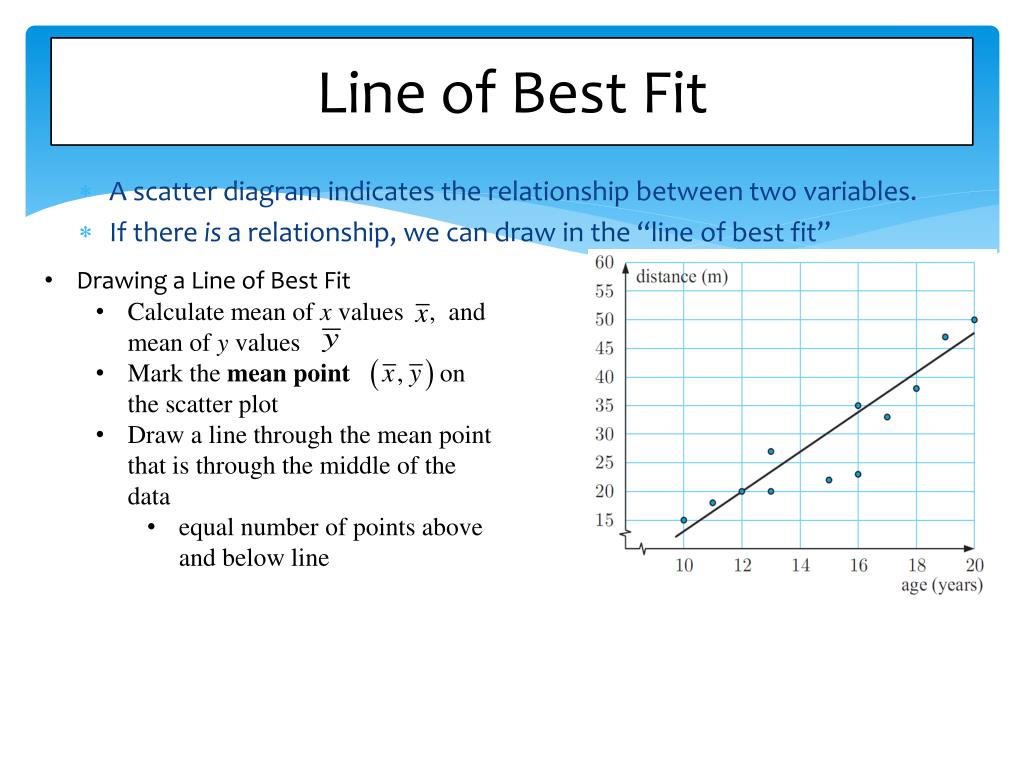
We will also see examples in this chapter where. Interpret the line of best fit. The line of best fit is used to express a relationship in a scatter plot of.

Choose stat > regression > fitted line plot. Plot line of best fit in base r. It’s the line that best shows the trend in the data given in a scatterplot.

Fitted line plots are a special type of scatterplot that displays the data points along with a fitted line for a simple regression model. This graph allows you to evaluate how well the. Under type of regression model, select quadratic.

A regression line is also. Complete the following steps to interpret a fitted line plot. The heights and weights of twenty children in.

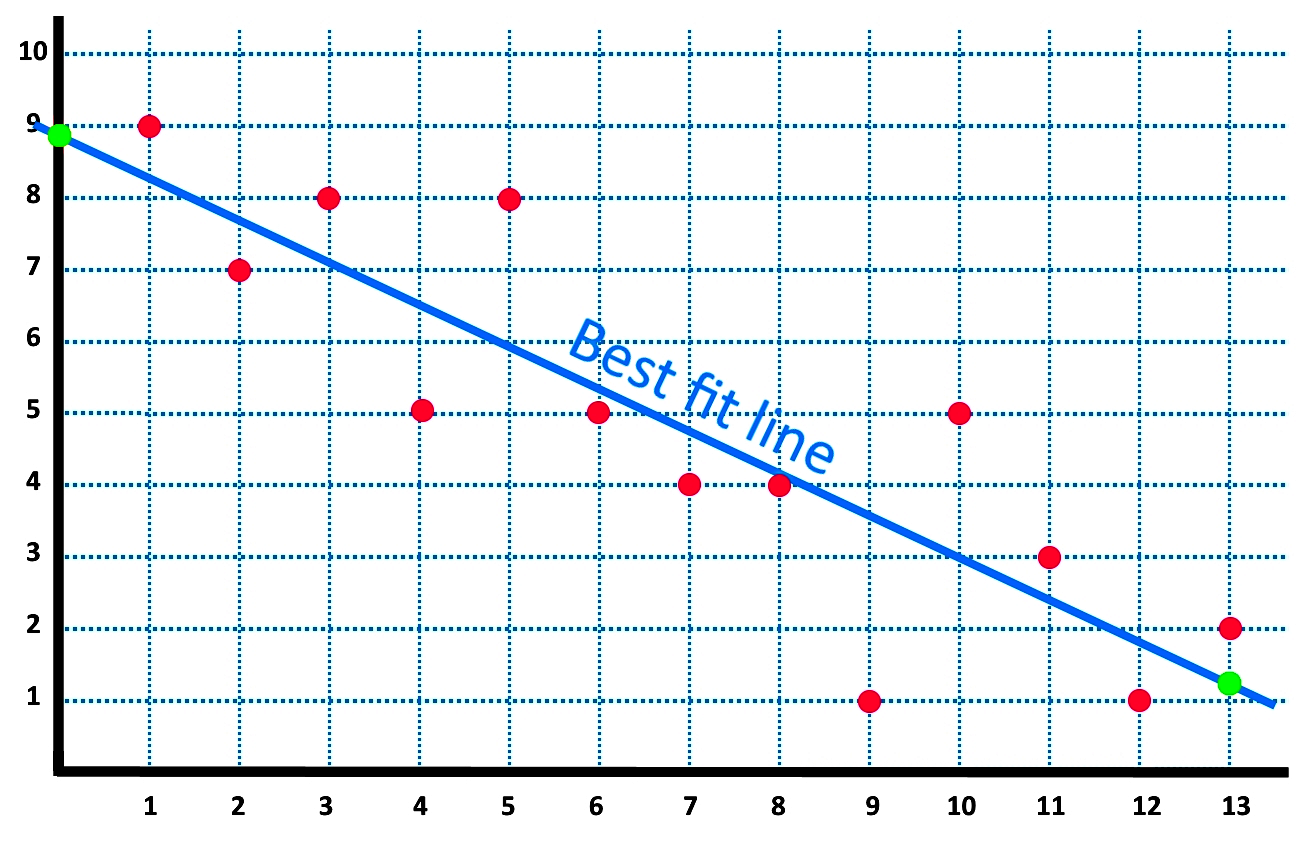
The most common way that we’ll do this is with a regression line. When drawing the line of best fit, use a transparent ruler to see how the line fits between all the points before you draw it. What is a line of best fit?

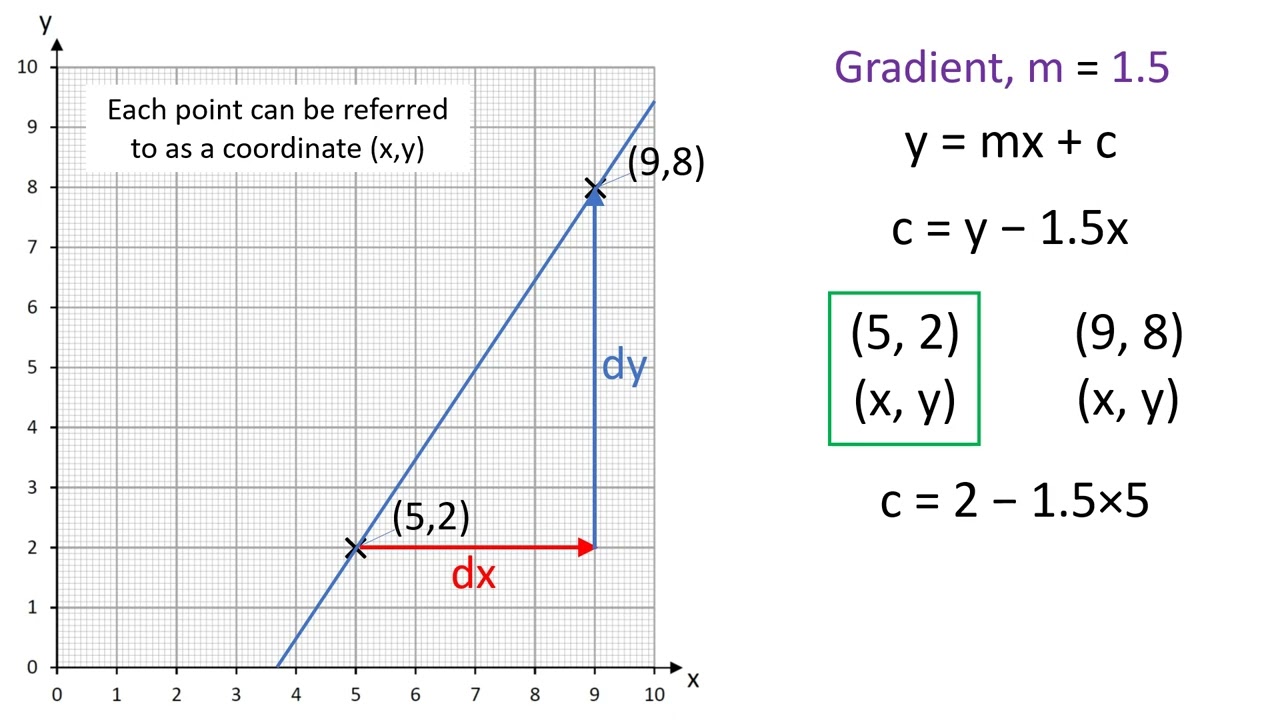
Use fitted line plot to display the relationship between one continuous predictor and a response. The plots on the left show the data, the center of the data $(\bar x,~\bar y)$ with a blue dot, the underlying data generating process with a dashed gray line, the. You can fit a linear, quadratic, or cubic model to the data.

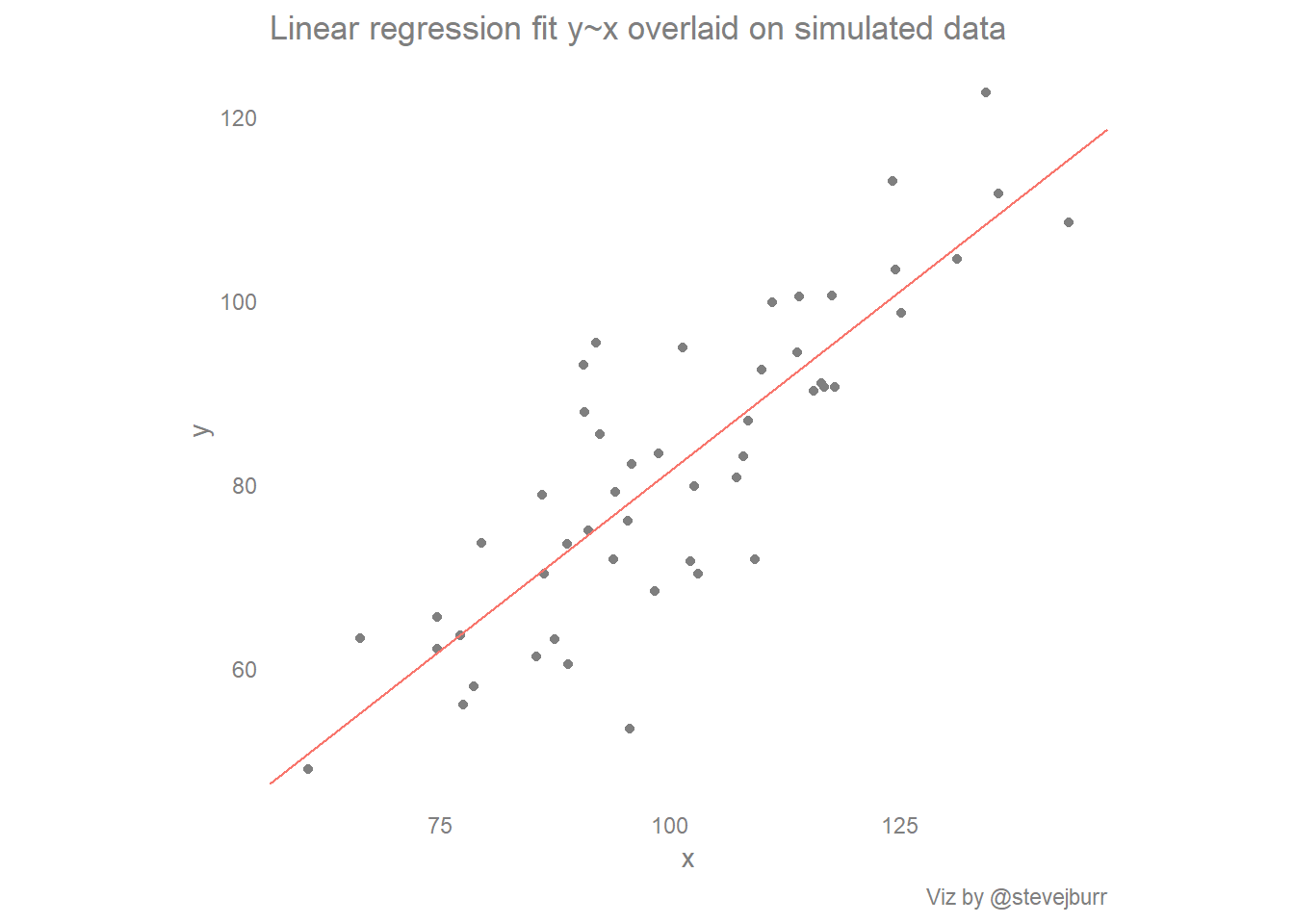
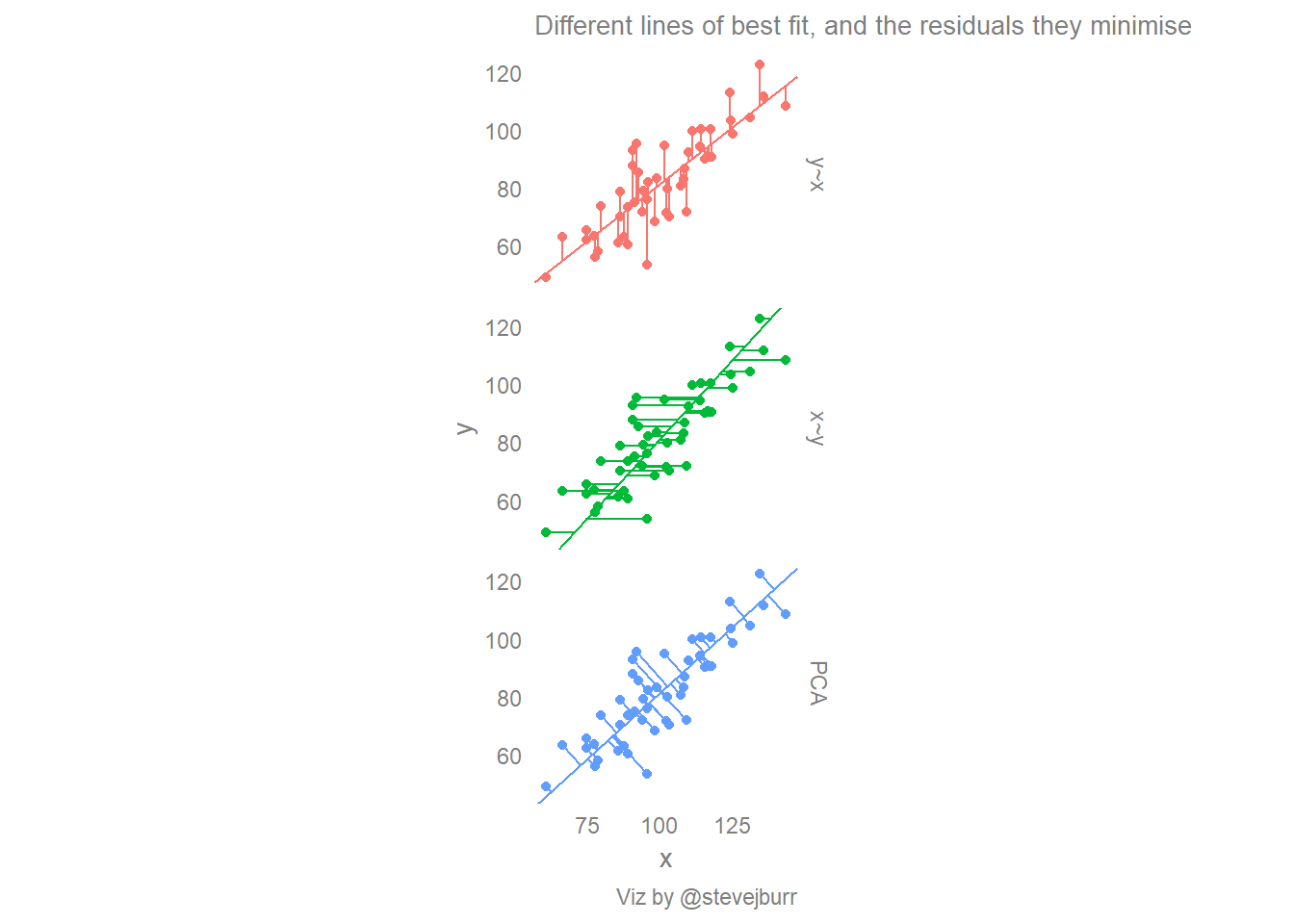
Create a line of best fit in excel. The plot includes the regression line, which represents the regression equation. Here's a possible description that mentions the form, direction, strength, and the presence of outliers—and mentions the context of the two variables: