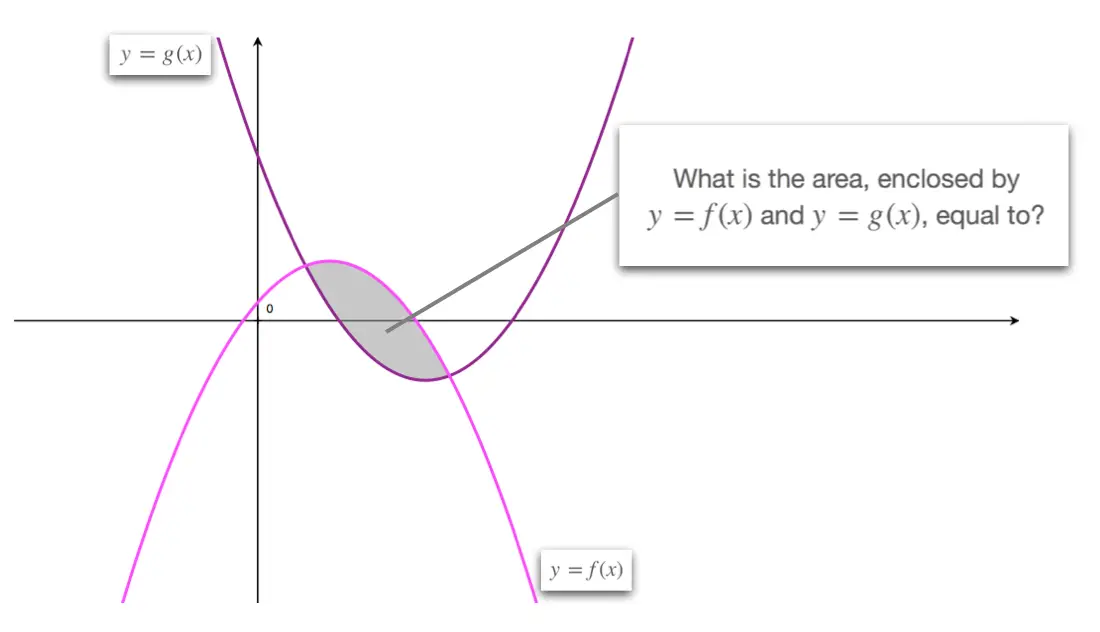
Beautiful Tips About Can Two Curves Be Parallel Excel Graph With Multiple Y Axis

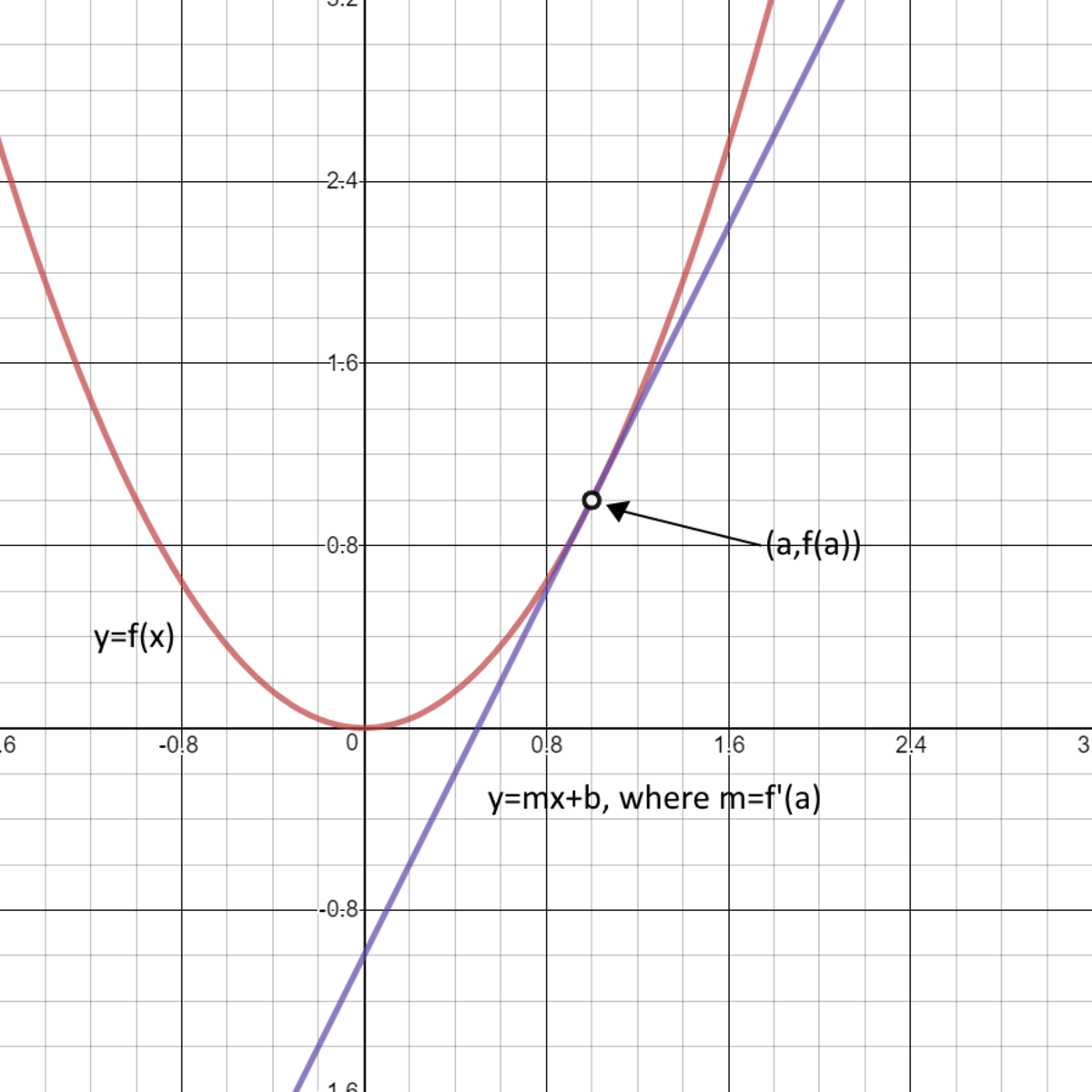
I have a simple parabola in the form $y = a + bx^2$.

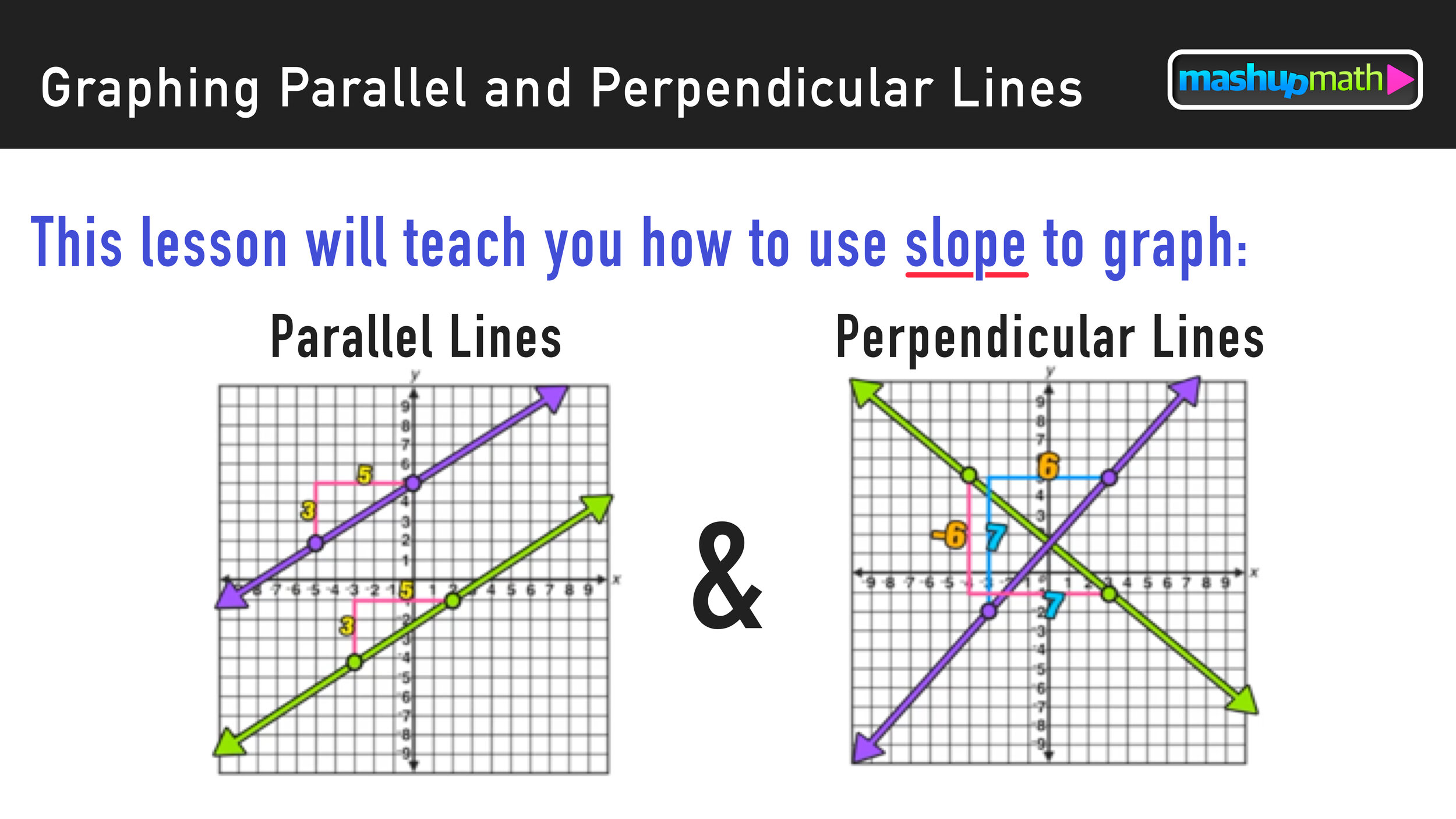
Can two curves be parallel. When two lines are parallel, it means that they will never intersect (assuming they're both infinite in length). As another extreme, two lines are called parallel if they do not intersect. Parallel always requires two lines to be equidistant and straight.

Draw large curves with a giant compass. Clamp the board and screw the compass to the workbench. This means that two curves can.

Y ∼ x} i x ≡ { y ∈ x: Applying the same to quadrics would mean testing for intersections. Is there something known as parallel circles?

But we can make the two lines curved and equidistant, as long as they don’t intersect with each other. 815 views 2 years ago math facts. The situation of straight lines is just a particular example of paralle.

It generalises the concept of parallel (straight) lines. Use a scrap to elevate the compass to the same height. Two curves are said to be parallel of one another if any curve normal to one is normal to the other;

My question is that can two concentric circles also be considered as parallel? Yes, curves in different planes can be parallel. By parallel i mean that there is an equal distance along a line perpendicular to the tangent to my curve at all points.

Mathematically parallel is unambiguosly defined. This property makes parallel lines much easier to work with from a mathematical perspective. A parallel of a curve is the envelope of a family of congruent circles centered on the curve.

Do not mistake with curves that are the translation of one another. It seems intuitively correct that β^′(a) =α′(s) β ^ ′ ( a) = α ′ ( s) because the tangent vectors of two parallel curves point in the same direction for each corresponding points on the two curves, but how can we show it rigorously? Ix ≡ {y ∈ x:

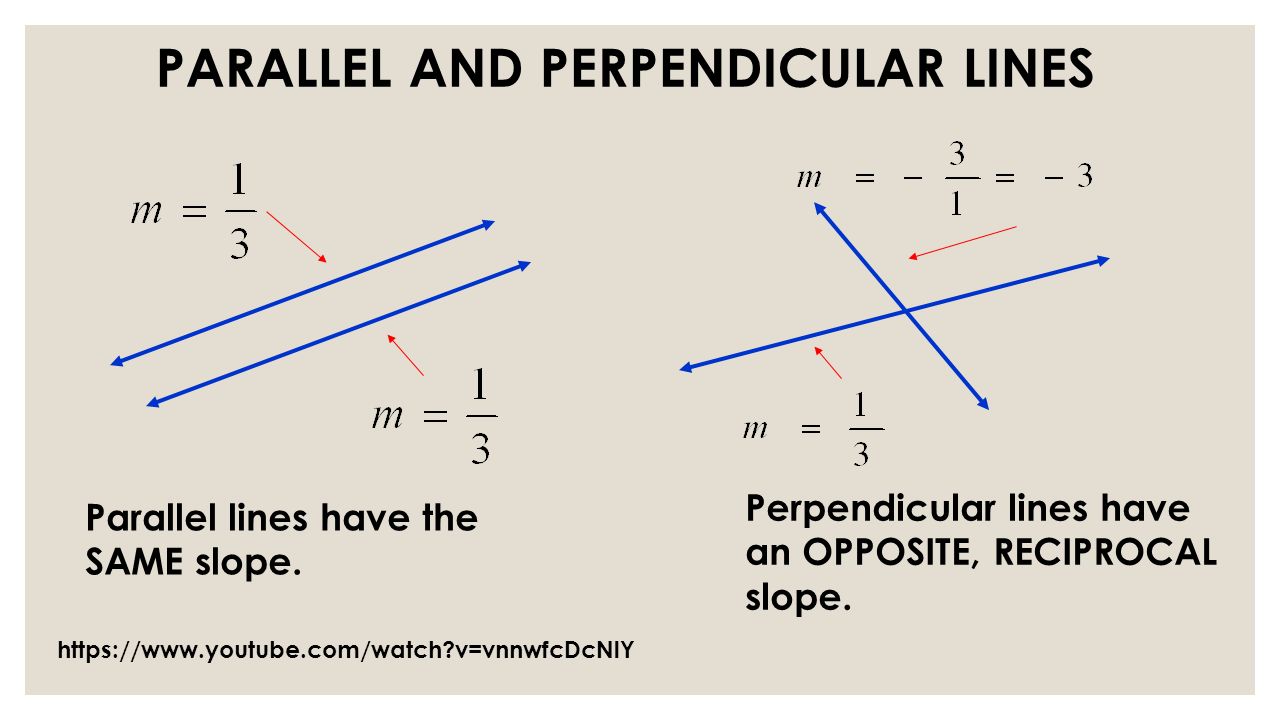
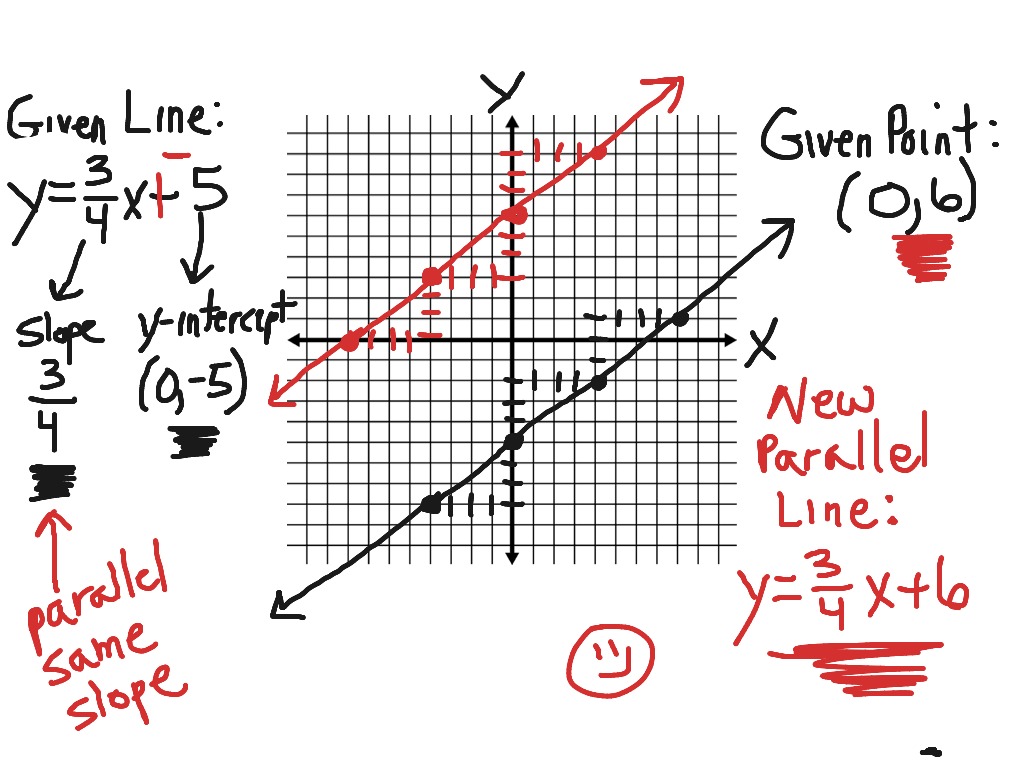
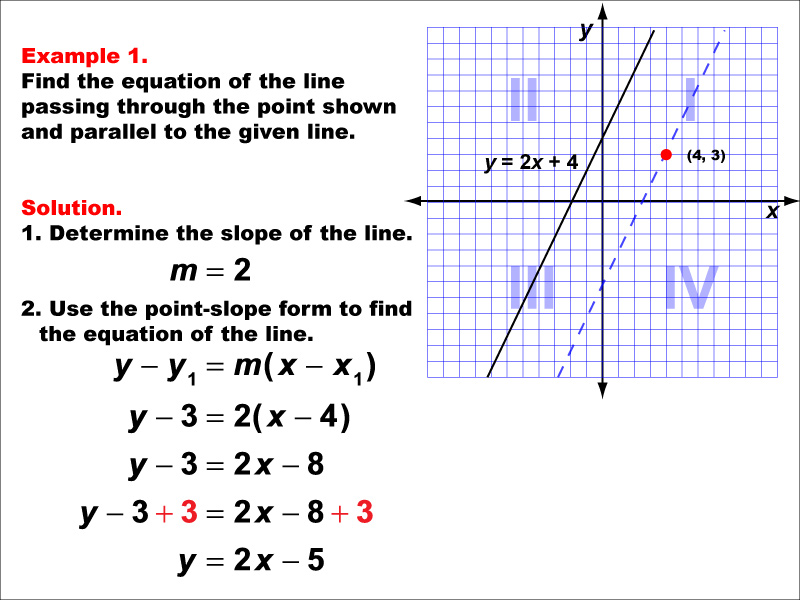
A curve distinct from yet equidistant from a line (or something else like a point) is an equidistant curve. Given a continuous preference relation ⪰ ⪰ over x = r2+ x = r + 2 where all sets: Two lines are parallel if they have the same gradient.

Alternatively, a parallel of a curve can be defined as the envelope of congruent circles whose centers lie on the curve. I am thinking that perhaps two tangents may be parallel at any given time. It can also be defined as a curve whose points are at a constant normal distance from a given curve.