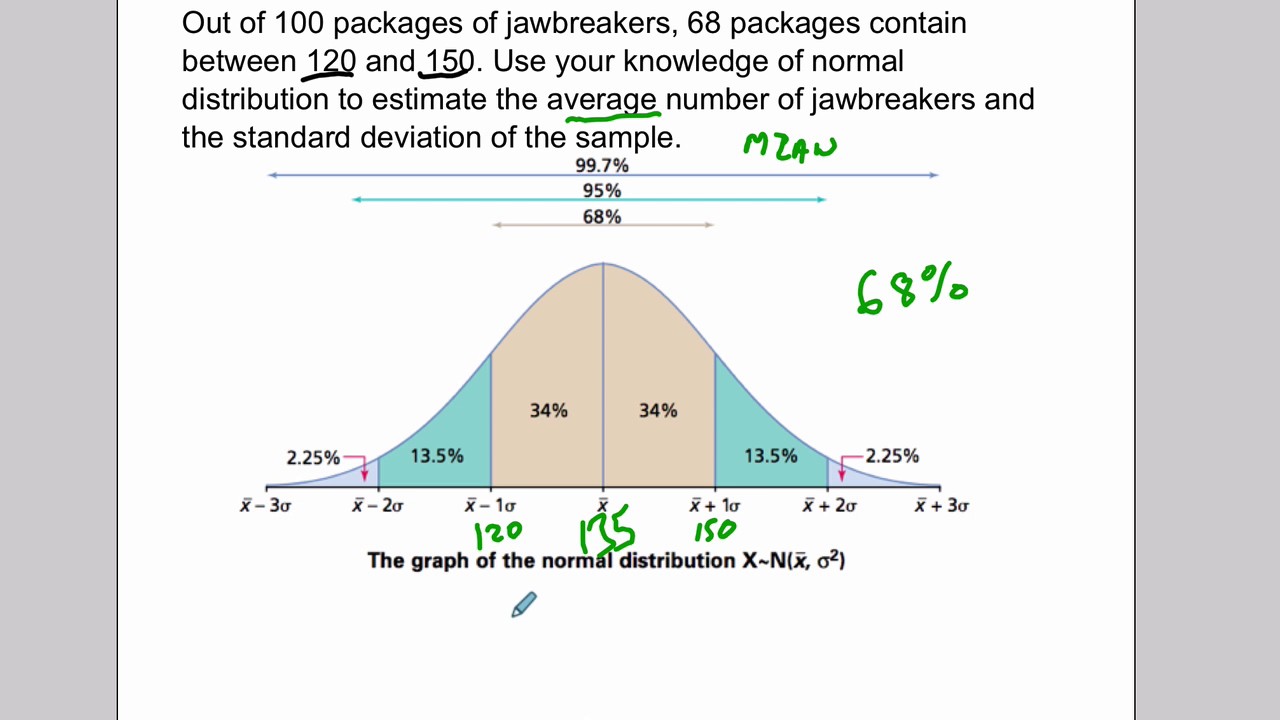
Beautiful Tips About Is The Normal Curve Smooth How To Change X And Y Axis Values In Excel

It reduces the noise to emphasize the.

Is the normal curve smooth. Suppose the curve is defined by the parametric equations. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the derivatives $\frac{d^nx}{dt^n}$ and $\frac{d^ny}{dt^n}$ exist. It intersects itself, has a cusp.

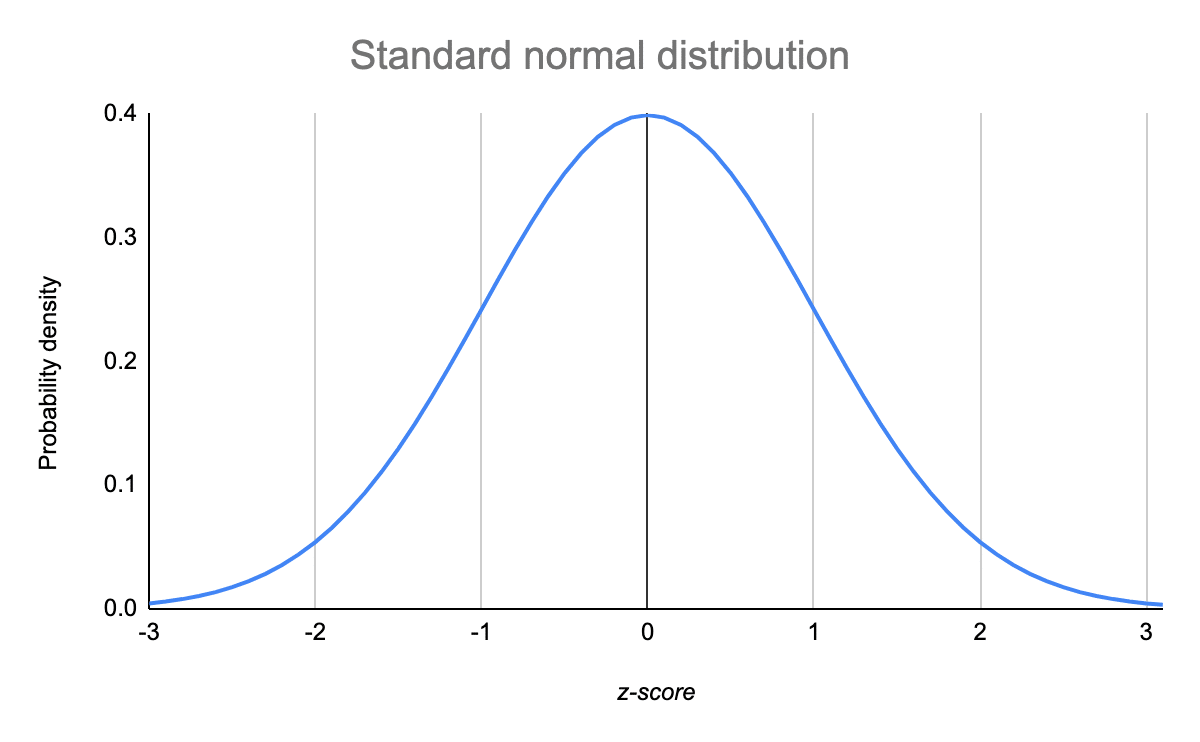
If the distribution of the test statistic is close to a normal distribution then we can use the normal curve to make simplifications in our calculation of that probability. A simple closed curve is piecewise smooth if it has a parametrization $\bfg$ as above, and there exists a finite (possibly empty) set of points $\{ t_1,\ldots, t_k\}\subset [a,b]$ such. The curve α(t) = (t3, t2) in the plane fails to be.

My original goal was to show for affine curves over $\mathbb{c}$, being normal is the same as smooth. The formula for the normal probability density function. A curve can fail to be smooth if:

If you import a curve from an instrument, you may wish to smooth the data to improve the appearance of a graph. Equivalently, we say that α is an immersion of i into r3. In the general context, regular is a property of a scheme (or a ring, or local ring), and smooth is a property of a morphism of schemes.

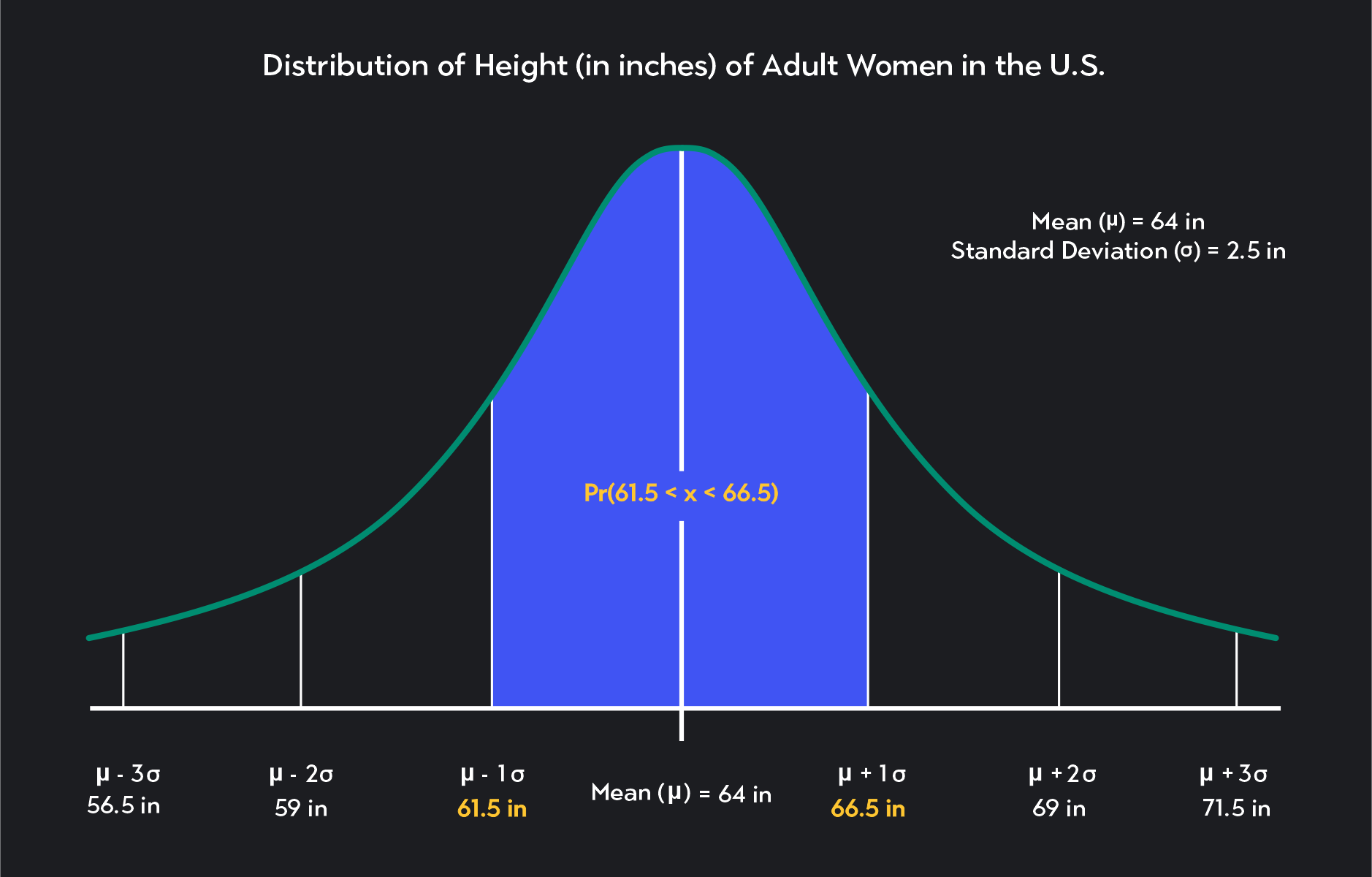
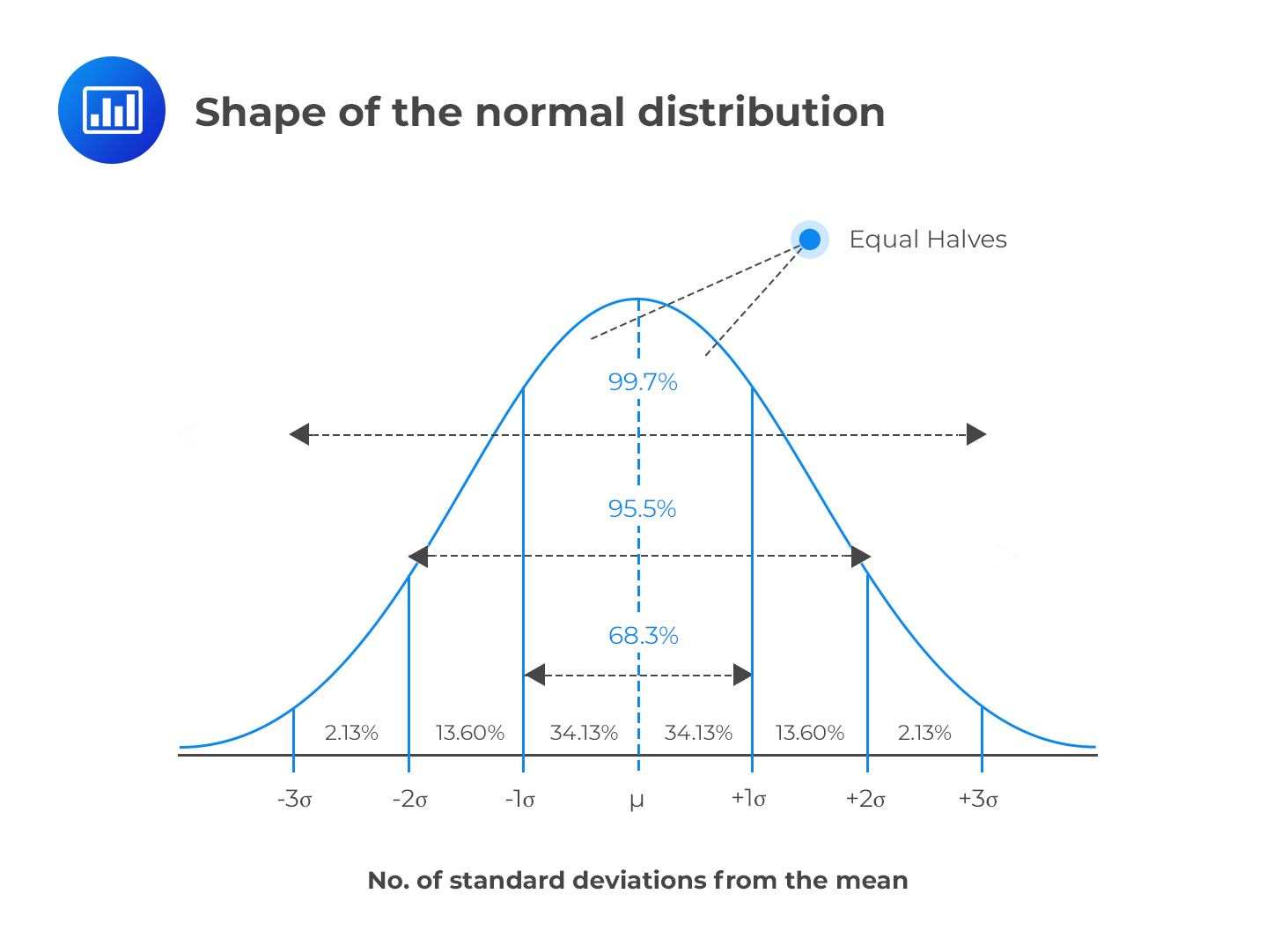
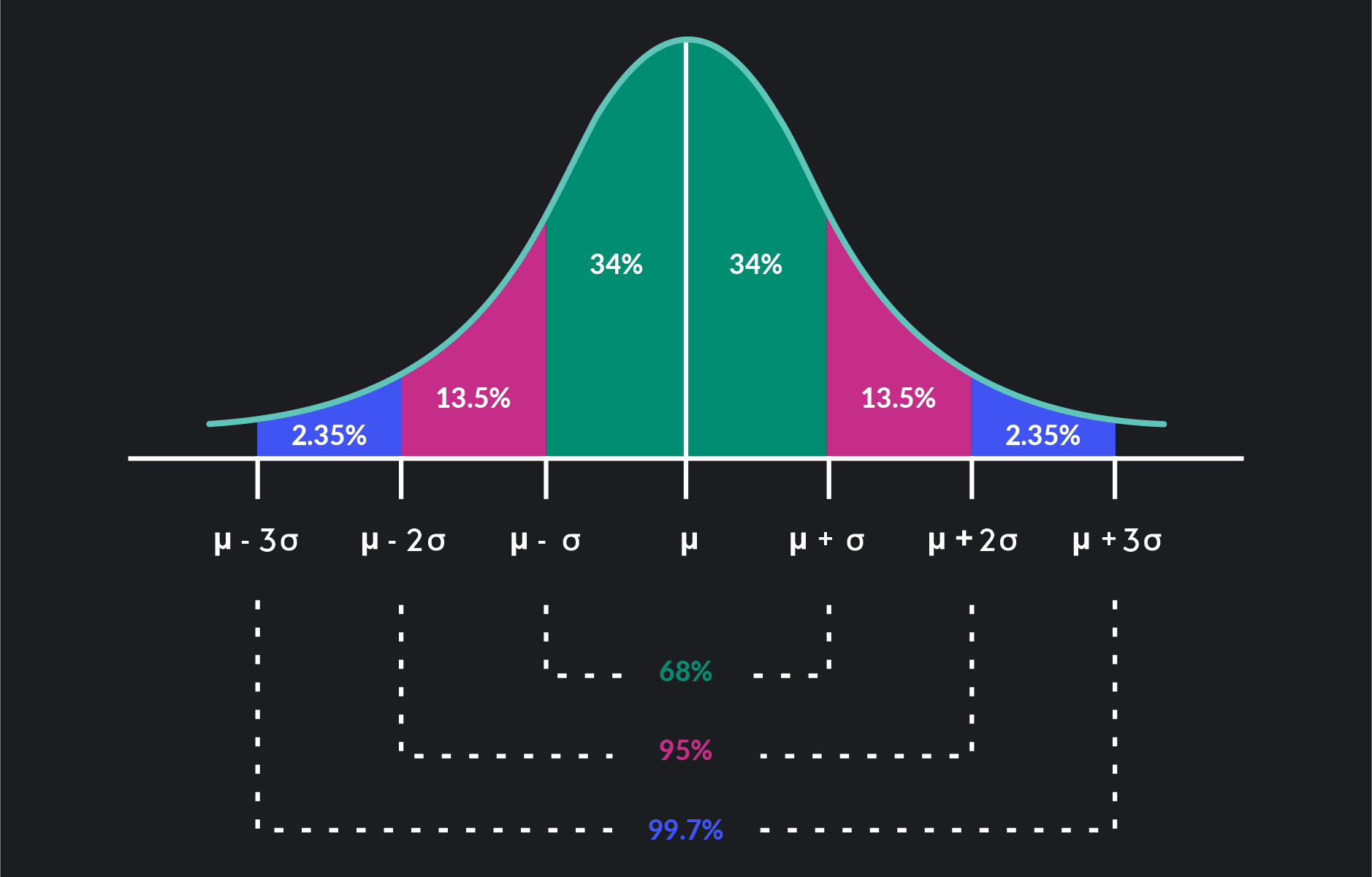
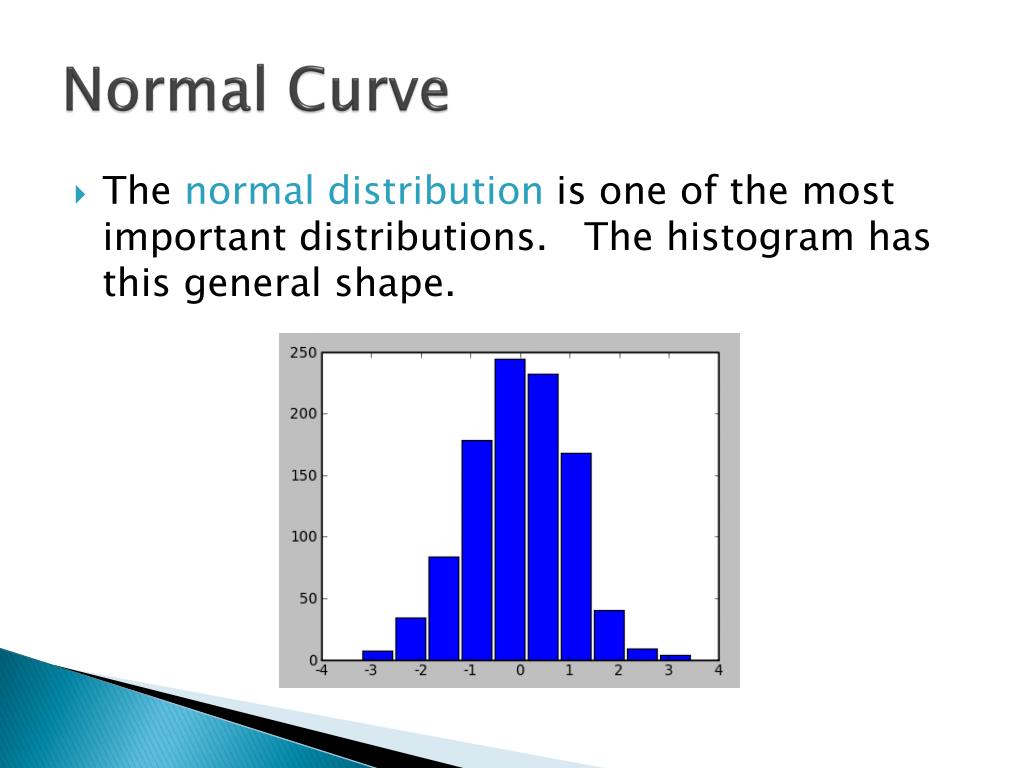
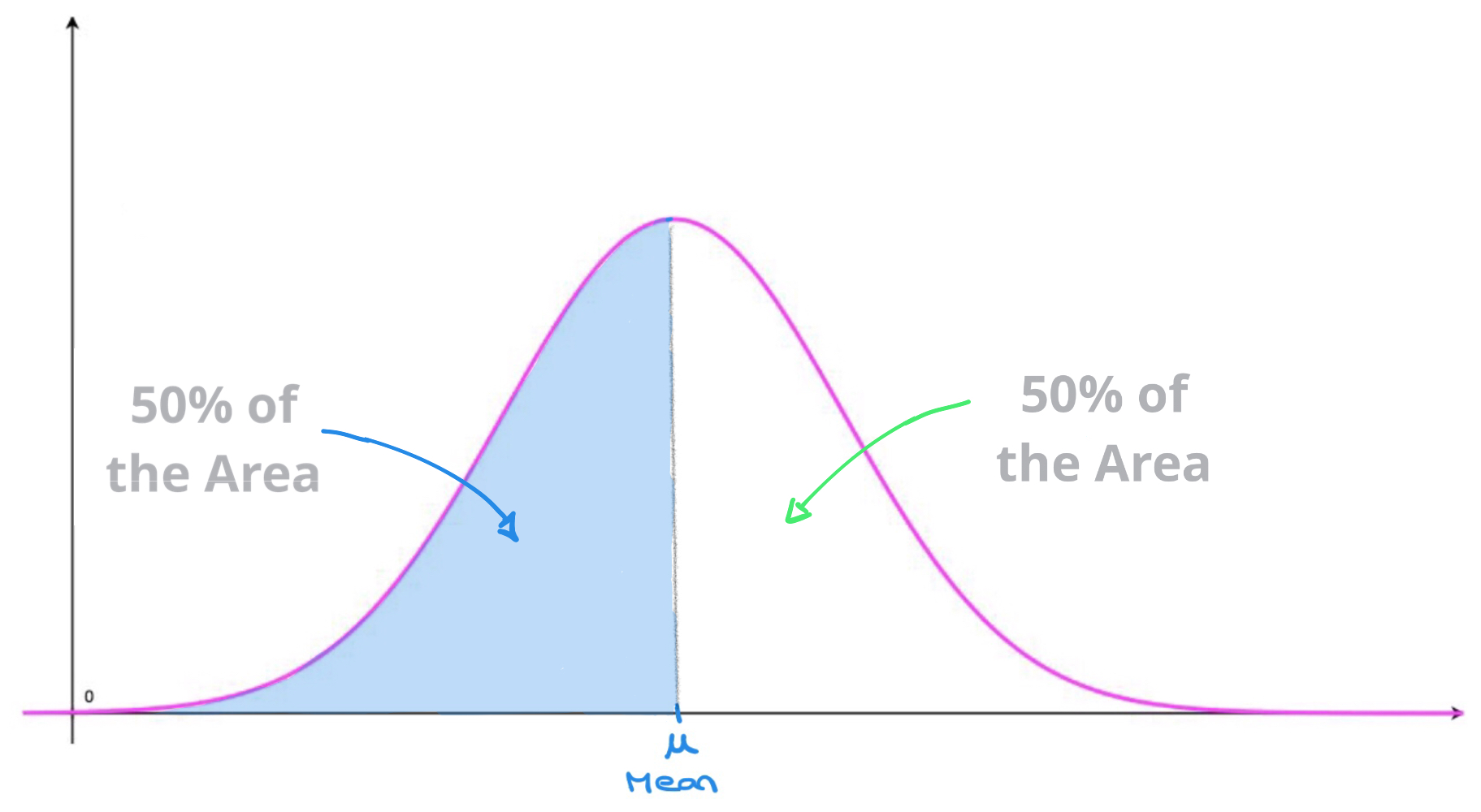
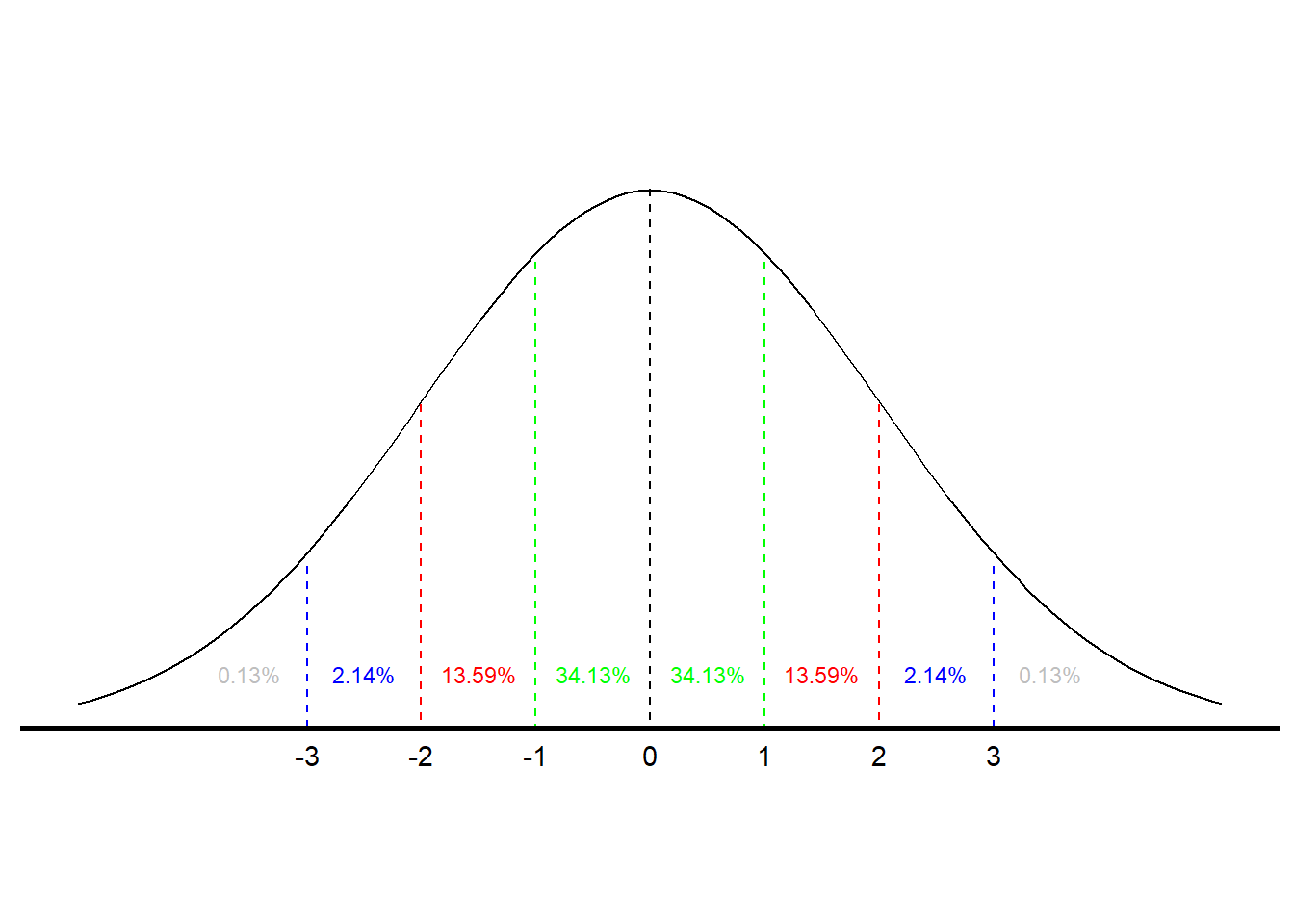
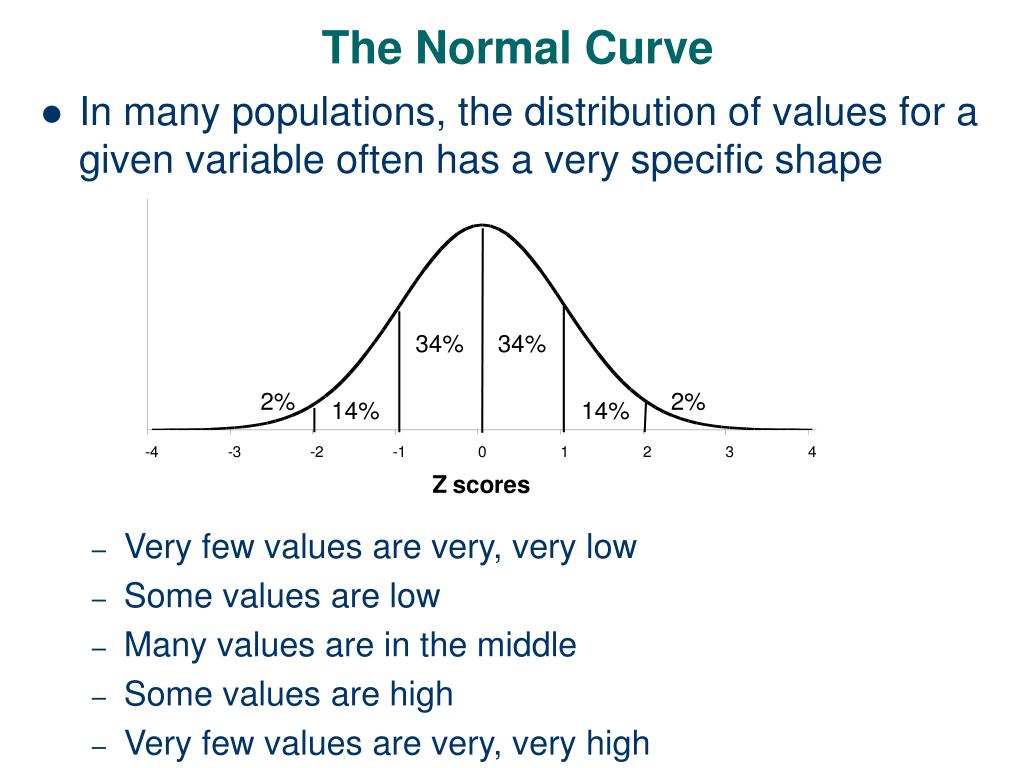
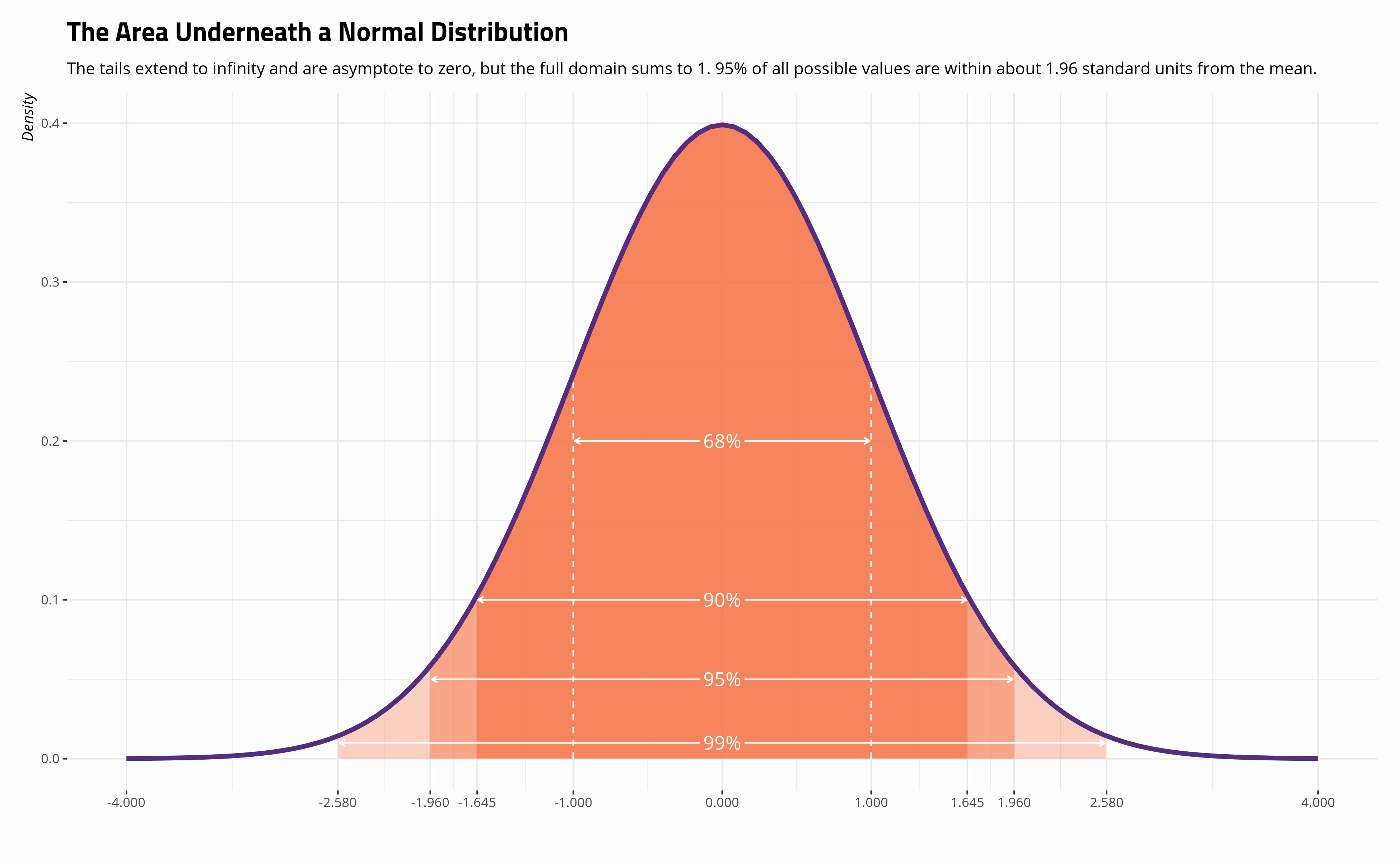
Let x/s x / s be a smooth, projective scheme of relative dimension one over a scheme s s (which we may assume is affine noetherian, but need not be reduced nor irreducible nor. The normal distribution is a probability distribution, so the total area under the curve is always 1 or 100%. (x, y, z) = (f(t), g(t), h(t)) ( x, y, z) = ( f ( t), g ( t), h ( t)), where t ∈ [a, b] t ∈ [ a, b] the curve is a smooth.

\what are all the curves of a given. A smooth curve α: (the point is that a normal noetherian local ring of dimension one is automatically regular, i.e.

Since you lose data when you smooth a. Giving us a start on the following questions: Smoothing is the process of removing random variations that appear as coarseness in a plot of raw time series data.

A curve $\mathbf{r}(t)$ is considered to be smooth if its derivative, $\mathbf{r}'(t)$, is continuous and nonzero for all values of $t$. A clear definition of smoothing of a 1d signal from scipy cookbook shows you how it works. This means a normal vector of a curve at a given point is.

The curvature is the length of the vector $$ \frac{\gamma'\times\gamma''}{\left|\gamma'\right|^3}\tag{2} $$ which is smooth because. For this, there are two pieces of lemma: In particular, a smooth curve is a.

I → r3 is said to be regular if α'(t) ≠ 0 for all t ∊ i. For curves over a field $k$, normal implies regular. A curve is smooth if every point has a neighbourhood where the curve is the graph of a differentiable function.