Divine Info About Is The Slope Of A Curved Line Constantly Changing D3 Chart

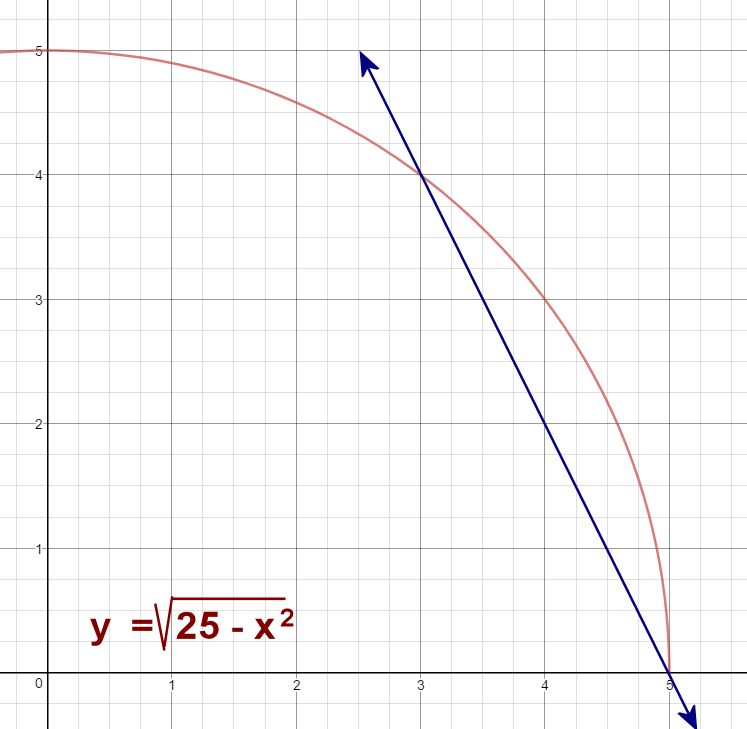
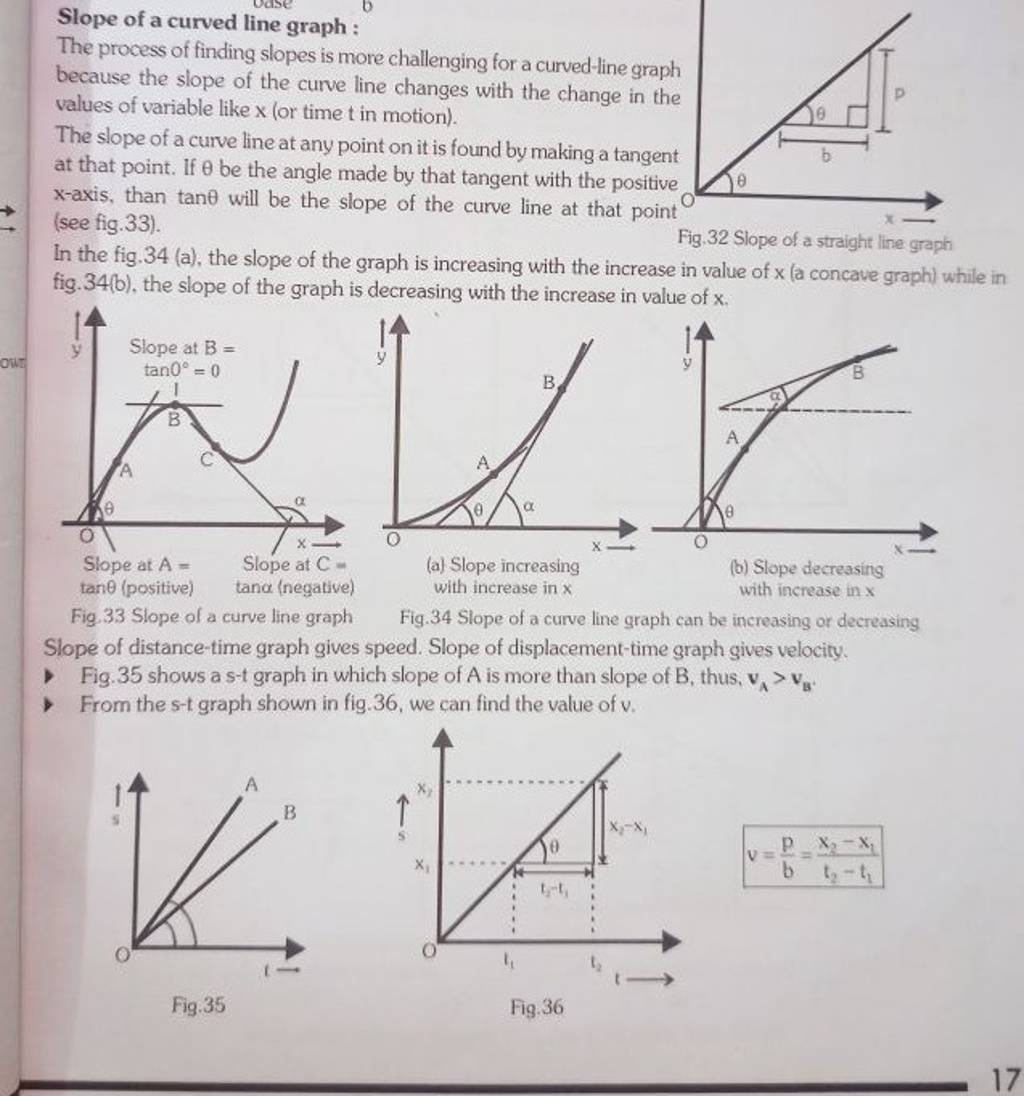
The situation here is that the gradient of the curve is constantly changing.

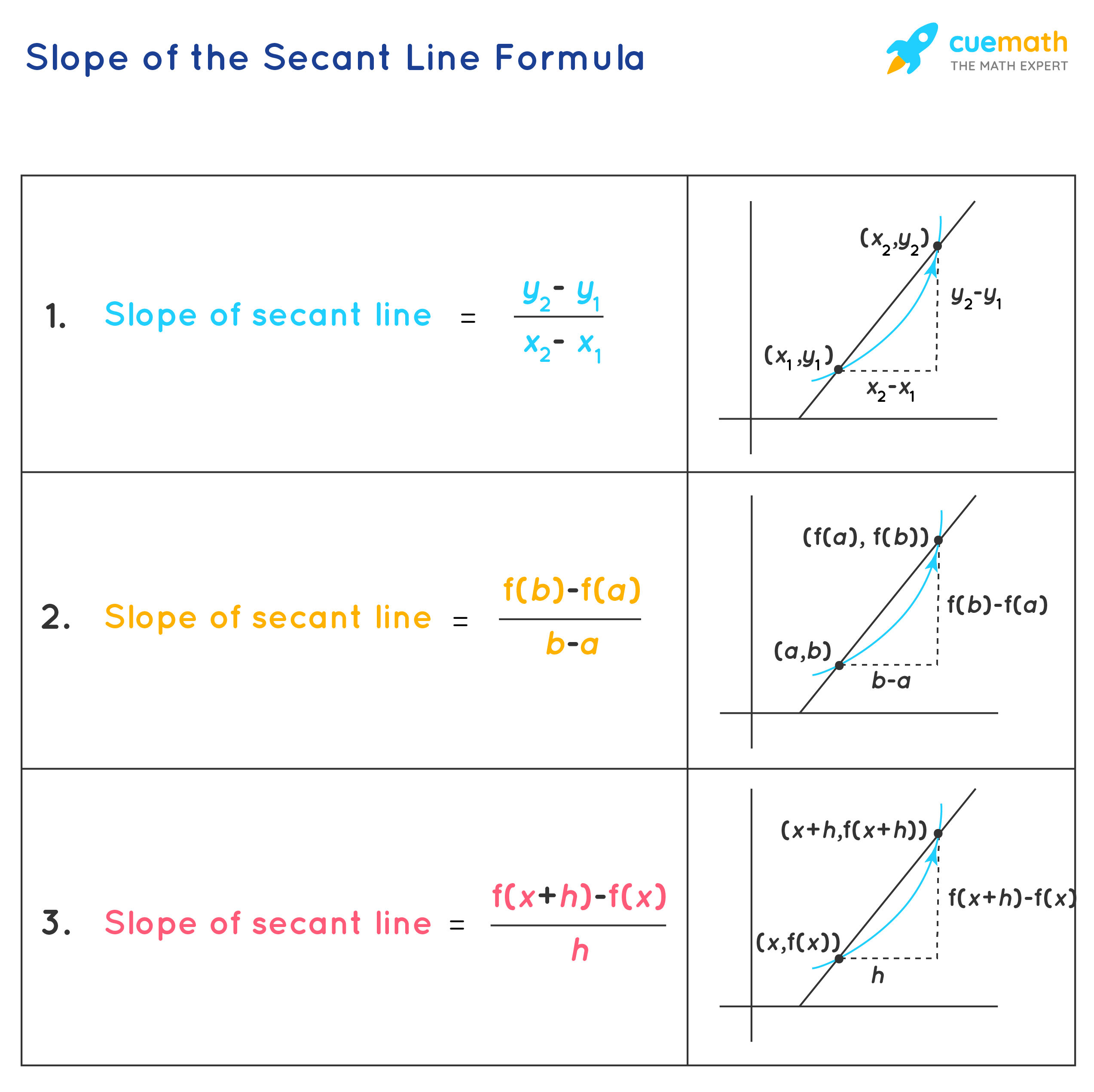
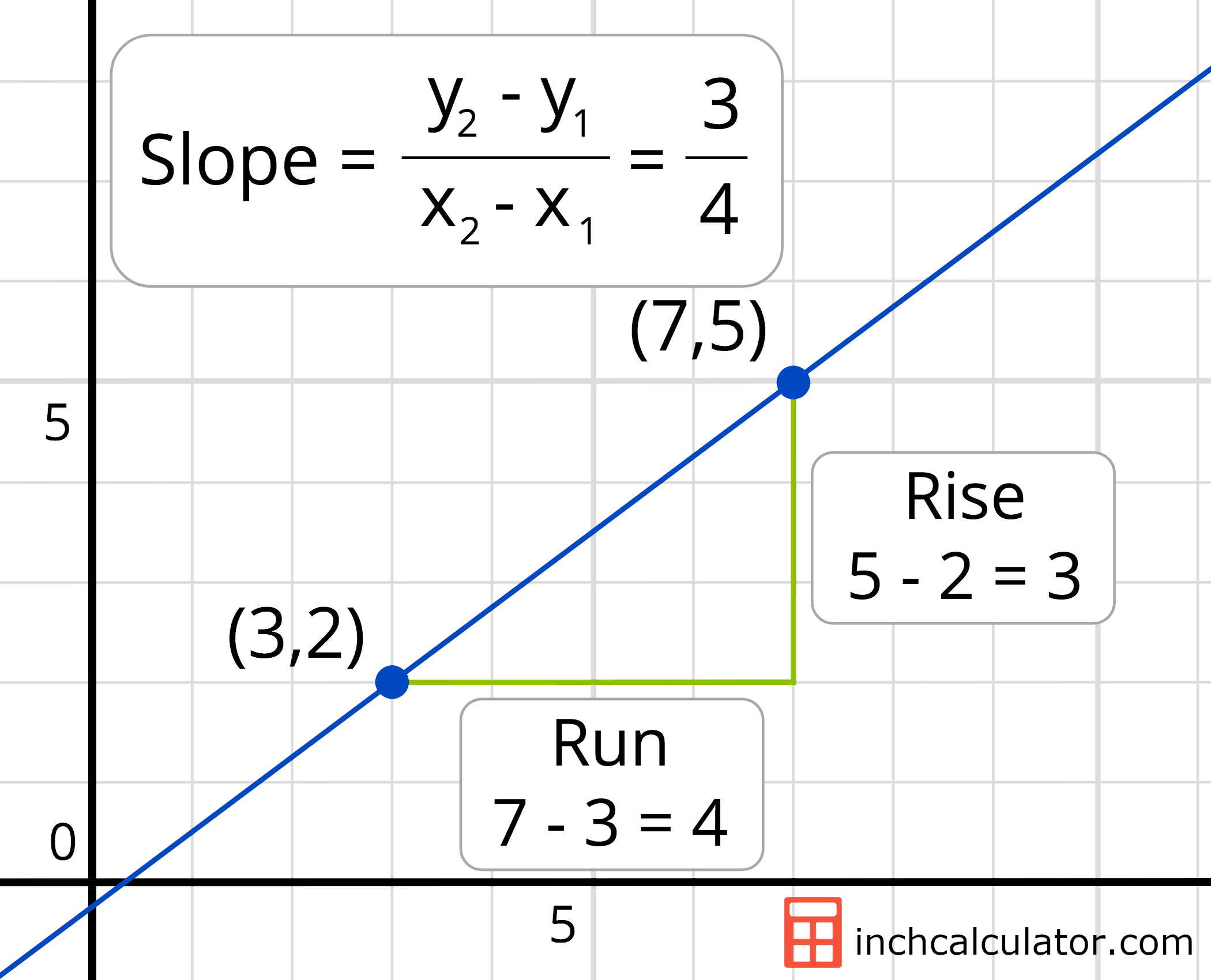
Is the slope of a curved line constantly changing. The slope of a line is rise over run. In this article, we will look at the slope of a straight line, and see how this concept can be applied to a curve. So, all we need to do is find the slope of the line through the points ( 11.4, 11.5) and ( 12.7, 15.4).

This can be interpreted as a measure of sensitivity''; The slope of any line remains constant along the line. They may start with a very small slope and begin curving sharply (either upwards or downwards) towards a large slope.

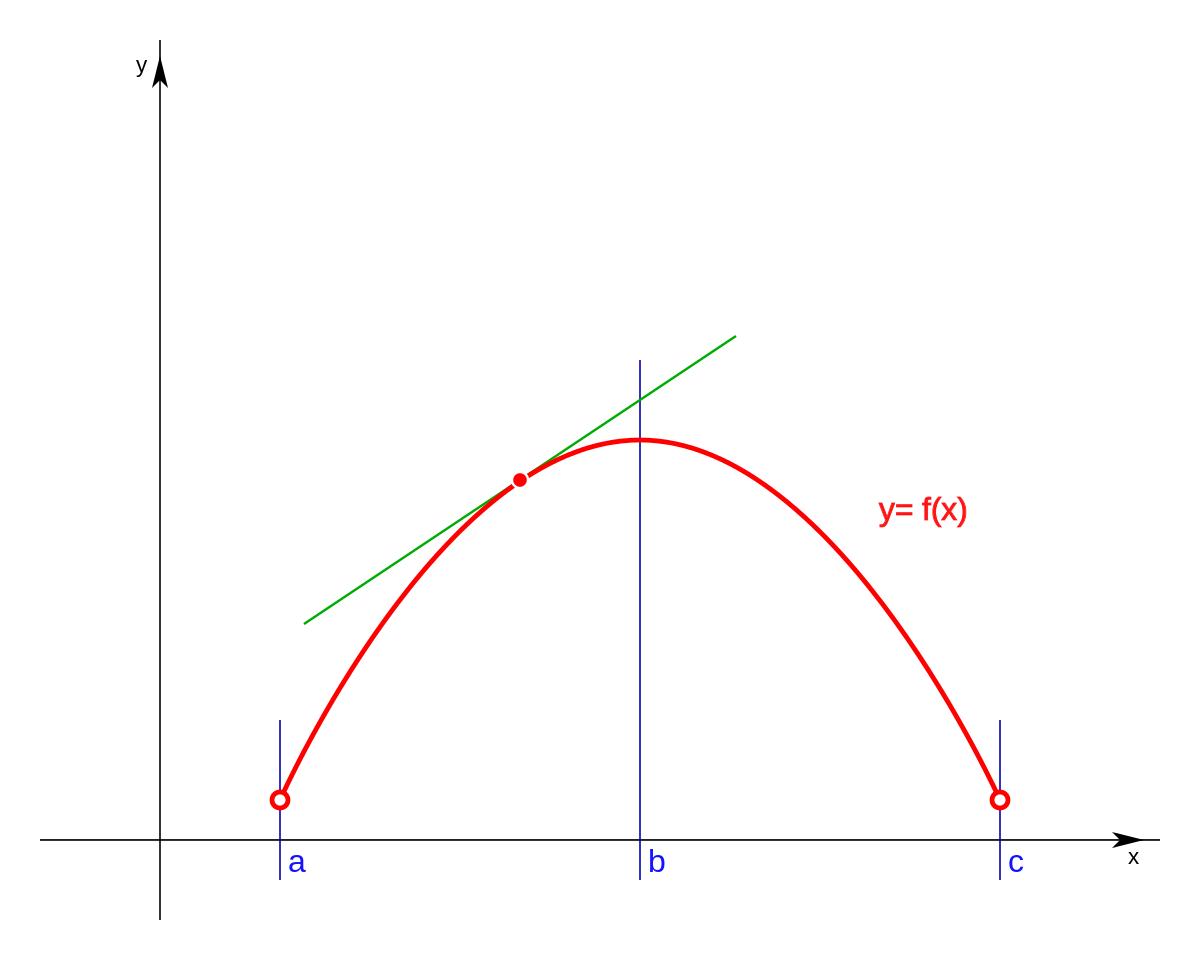
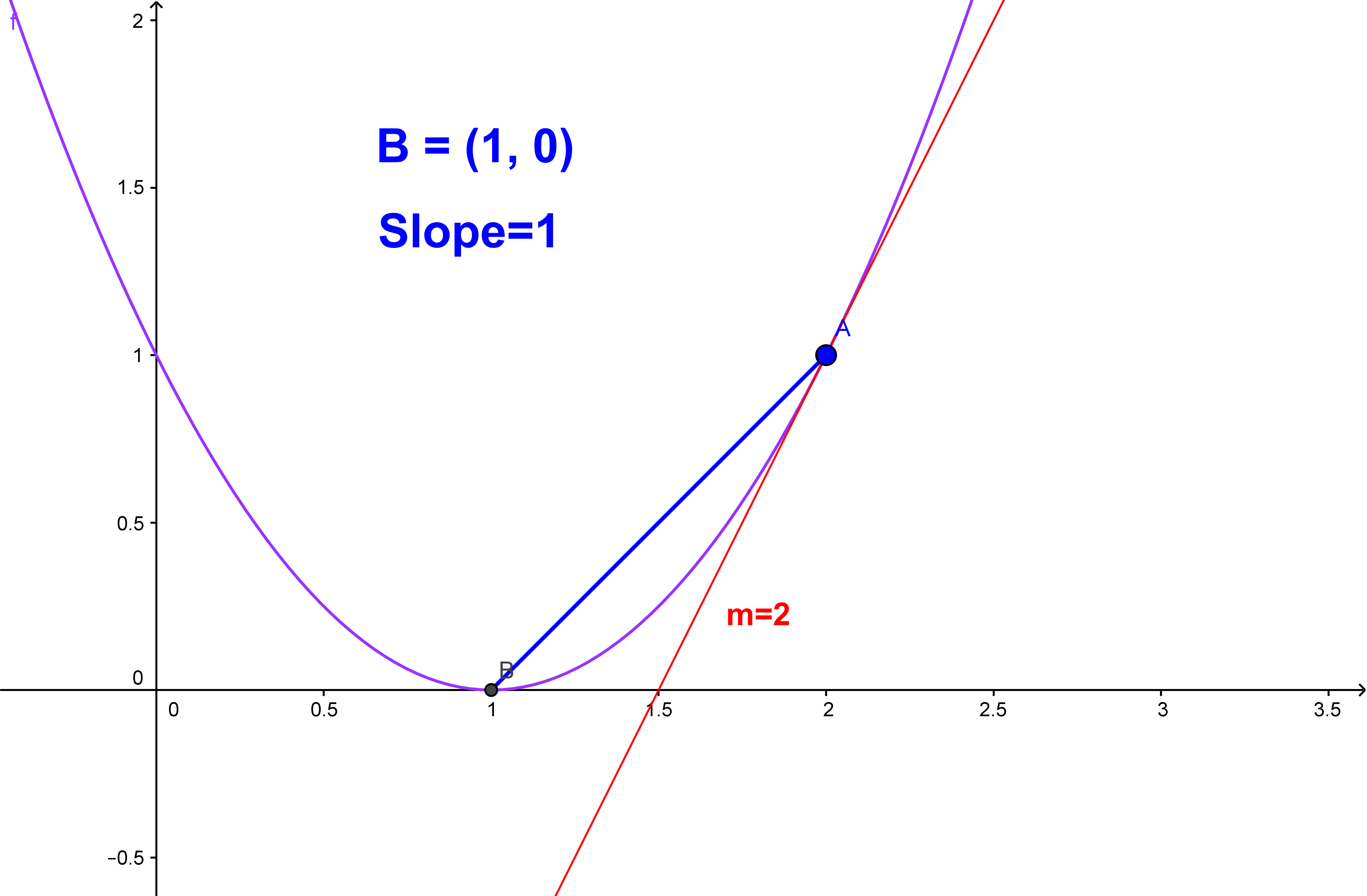
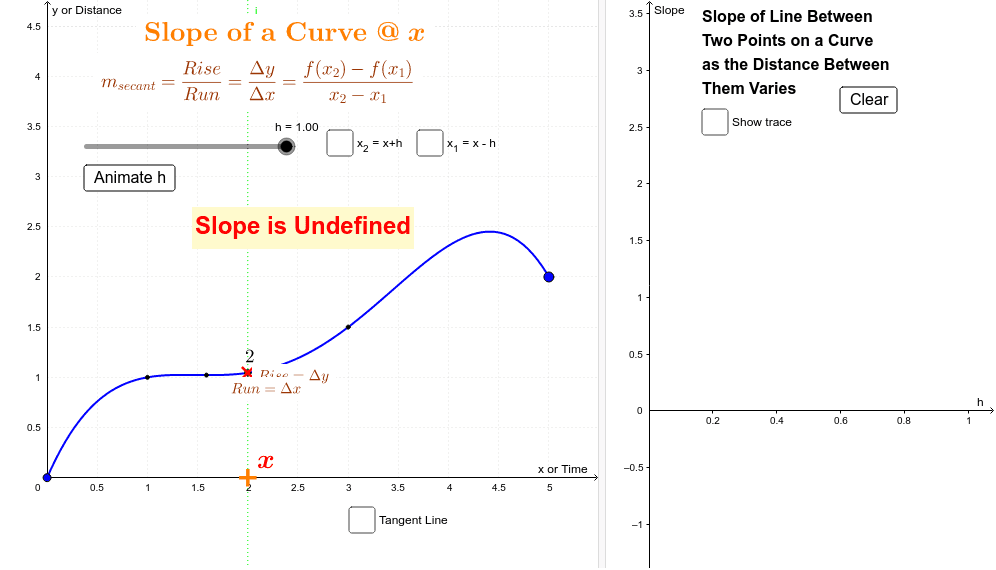
The first thing to realize is that each solution is a point on the line. A tangent line just barely “kisses” a curve at a single point. Here x1 and x2 are given to you, but you need to calculate y1 and y2.

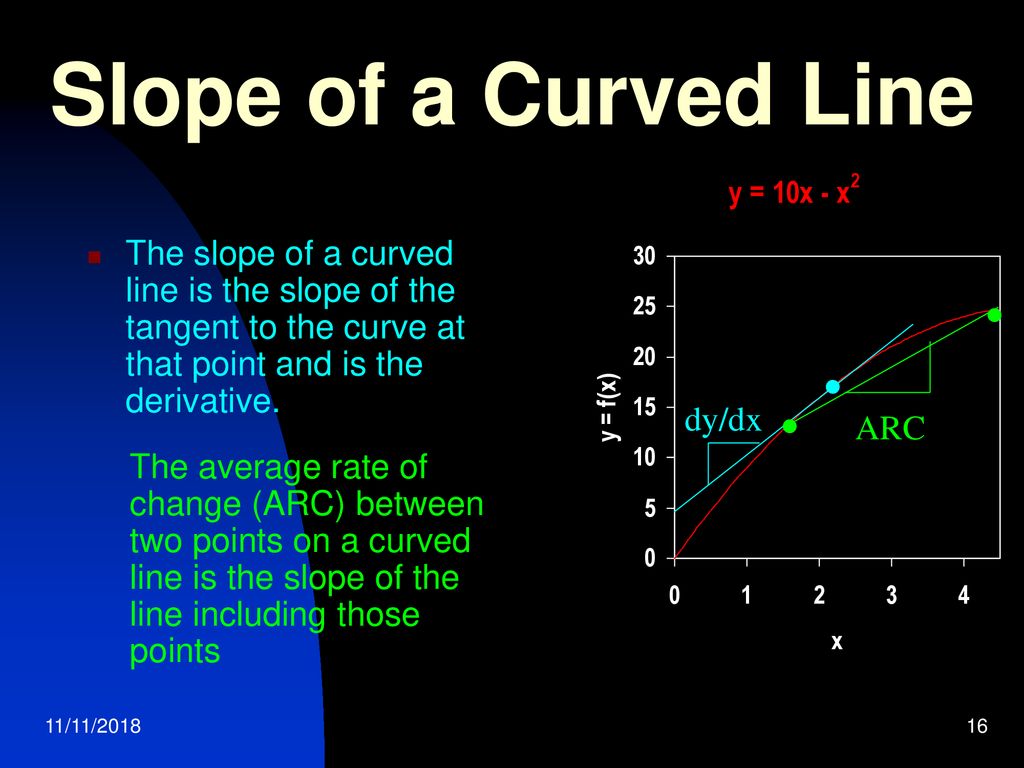
The slope of a smooth curve at a pont on the curve is defined as the slope of the tangent line at that point. So what you want to do is see what happens as your change of x gets smaller and smaller and smaller. In either case, the curved line of changing slope is a sign of accelerated motion (i.e., changing velocity).

We can clearly see that the slope of the curve is changing; Slope of a line. If we were using calculus, the slope of a curved line could be calculated.

But finding the slope of the straight line that joins p and q just requires the formula you quoted. The slope of the line is positive, corresponding to the positive acceleration. Since the tangent is a straight line, we can determine the value of its gradient by using the techniques outlined above.

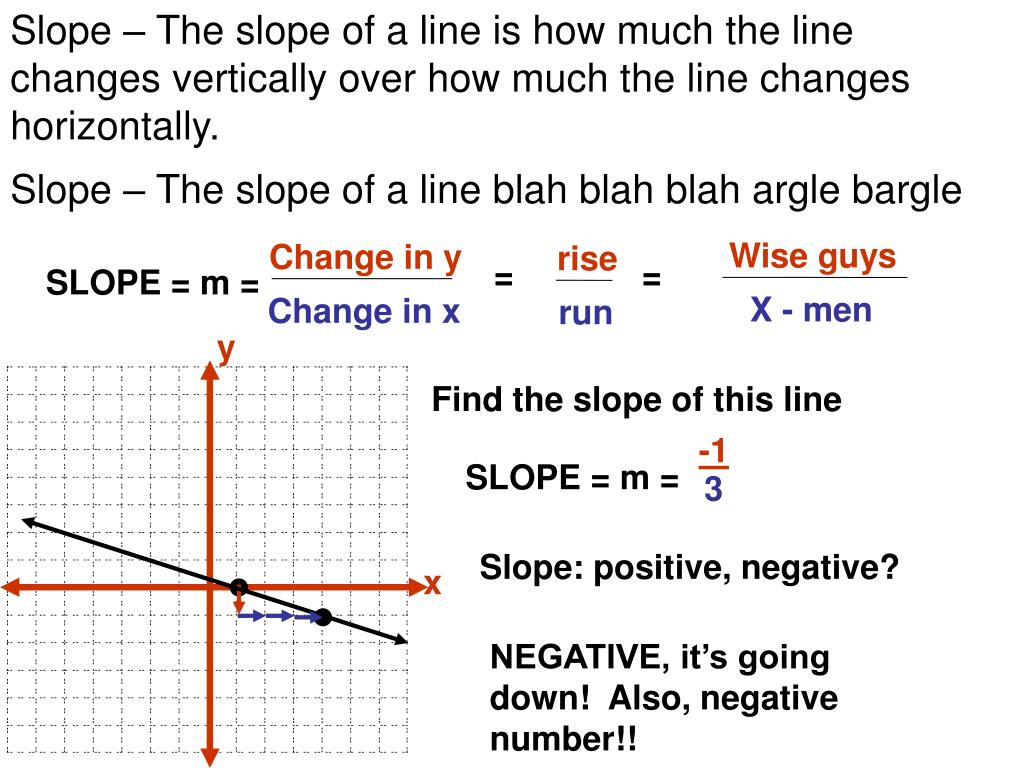
Mathematically, the slope of a curve is represented by rise over run or the change in the variable on the vertical axis divided by the change in the variable on the horizontal axis. That means that the slope is increasing. Learn how to calculate the slope of the line in a graph by finding the change in y and the change in x.

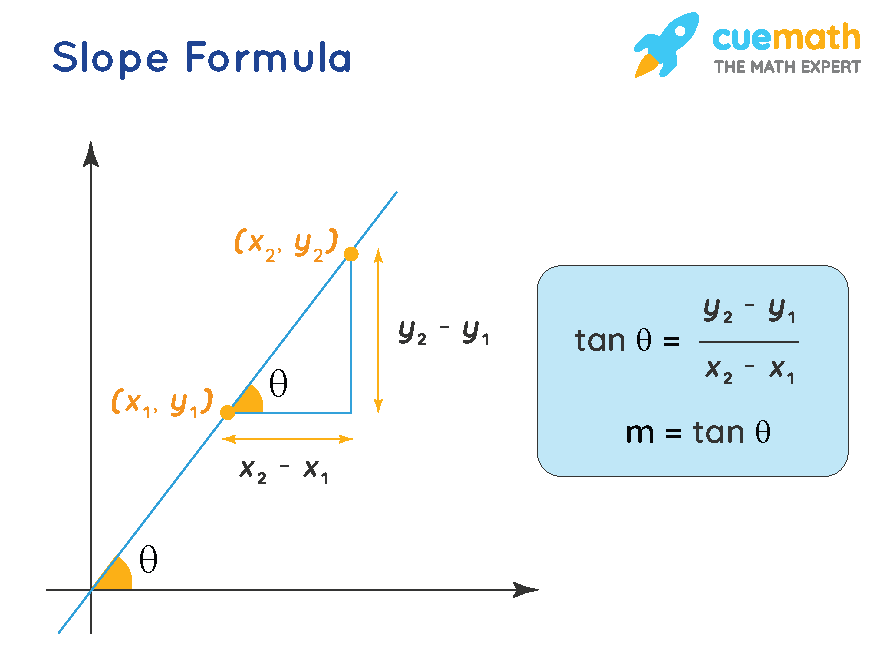
At any point, it is equal to the gradient of the tangent drawn to the curve at that point, such as that shown at p. Slope describes the steepness of a line. The slope of a line is \(m=\dfrac{\text{rise}}{\text{run}}\).

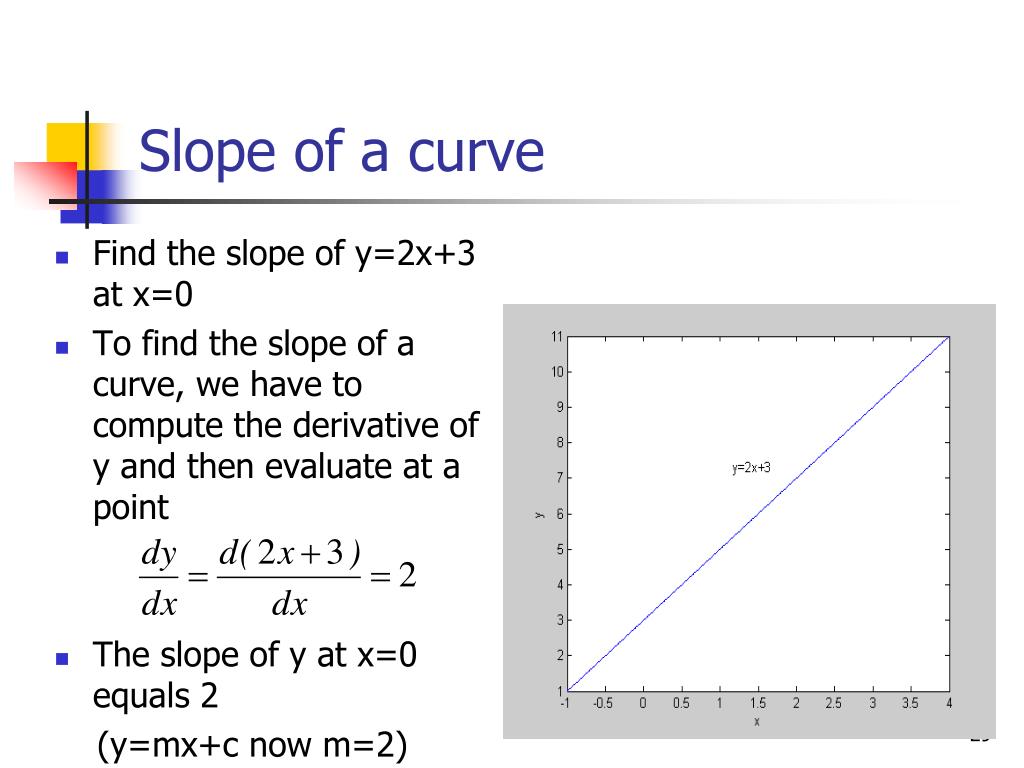
Created by sal khan and monterey institute for technology and education. Slope can be calculated either by looking at the graph of a line or by using the coordinates of any two points on a line. In the case of a straight line \(y=mx+b\), the slope \(m=\delta y/\delta x\) measures the change in \(y\) per unit change in \(x\).

How to find the slope of a line from its graph using \(m=\dfrac{\text{rise}}{\text{run}}\). (the independent variable of a linear function is raised no higher than the first power.) And we're asked to find the slope of the graph of that equation.